ЬтФПФкШн
ЁОЬтФПЁПШєвЛИіКЏЪ§ЕБздБфСПдкВЛЭЌЗЖЮЇФкШЁжЕЪБЃЌКЏЪ§БэДяЪНВЛЭЌЃЌЮвУЧГЦетбљЕФКЏЪ§ЮЊЗжЖЮКЏЪ§ЃЌЯТУцЮвУЧВЮеебЇЯАКЏЪ§ЕФЙ§ГЬгыЗНЗЈЃЌЬНОПЗжЖЮКЏЪ§yЃН ЕФЭМЯѓгыаджЪЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
ЕФЭМЯѓгыаджЪЃЌЬНОПЙ§ГЬШчЯТЃЌЧыВЙГфЭъећЃЎ
ЃЈ1ЃЉСаБэЃК
x | Ё | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | Ё |
y | Ё | 3 | m | 1 | 0 | 1 | 2 | 1 | n |
| Ё |
ЦфжаЃЌmЃНЁЁ ЃЌnЃНЁЁ ЁЁЃЎ
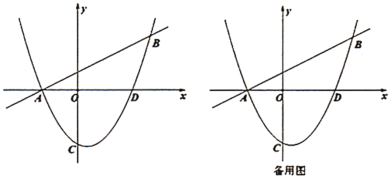
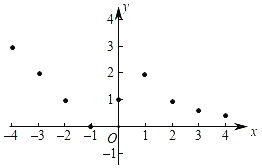
ЃЈ2ЃЉУшЕуЃКдкЦНУцжБНЧзјБъЯЕжаЃЌвдздБфСПxЕФШЁжЕЮЊКсзјБъЃЌвдЯргІЕФКЏЪ§жЕyЮЊзнзјБъЃЌУшГіЯргІЕФЕуЃЌШчЭМЫљЪОЃЌЧыЛГіКЏЪ§ЕФЭМЯѓЃЎ
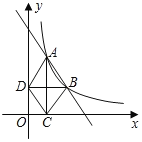
ЃЈ3ЃЉбаОПКЏЪ§ВЂНсКЯЭМЯѓгыБэИёЃЌЛиД№ЯТСаЮЪЬтЃК
ЂйЕуAЃЈ![]() ЃЌy1ЃЉЃЌBЃЈ5ЃЌy2ЃЉЃЌCЃЈx1ЃЌ
ЃЌy1ЃЉЃЌBЃЈ5ЃЌy2ЃЉЃЌCЃЈx1ЃЌ![]() ЃЉЃЌDЃЈx2ЃЌ6ЃЉдкКЏЪ§ЭМЯѓЩЯЃЌдђy1ЁЁ y2ЃЌx1ЁЁ x2ЃЛЃЈЬюЁАЃОЁБЃЌЁАЃНЁБЛђЁАЃМЁБЃЉ
ЃЉЃЌDЃЈx2ЃЌ6ЃЉдкКЏЪ§ЭМЯѓЩЯЃЌдђy1ЁЁ y2ЃЌx1ЁЁ x2ЃЛЃЈЬюЁАЃОЁБЃЌЁАЃНЁБЛђЁАЃМЁБЃЉ
ЂкЕБКЏЪ§жЕyЃН1ЪБЃЌЧѓздБфСПxЕФжЕЃЛ
ЃЈ4ЃЉШєжБЯпyЃНЉx+bгыКЏЪ§ЭМЯѓгаЧвжЛгавЛИіНЛЕуЃЌЧыжБНгаДГіbЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉ2ЃЌ![]() ЃЛЃЈ2ЃЉШчЭМЫљЪОЃЌМћНтЮіЃЛЃЈ3ЃЉЂйЃОЃЌЃОЃЛЂкxЃН0ЛђxЃНЉ2ЛђxЃН2ЃЛЃЈ4ЃЉЉ1ЃМbЃМ2
ЃЛЃЈ2ЃЉШчЭМЫљЪОЃЌМћНтЮіЃЛЃЈ3ЃЉЂйЃОЃЌЃОЃЛЂкxЃН0ЛђxЃНЉ2ЛђxЃН2ЃЛЃЈ4ЃЉЉ1ЃМbЃМ2![]() ЛђbЃО3ЃЎ
ЛђbЃО3ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋx=Љ3ДњШыyЃН|x+1|ЕУmЕФжЕЃЛНЋxЃН3ДњШыyЃН![]() жаЕУnЕФжЕЃЛ
жаЕУnЕФжЕЃЛ
ЃЈ2ЃЉгУЦНЛЌЕФЧњЯпСЌНгзјБъЯЕжаУшЕФЕуПЩЕУЃЛ
ЃЈ3ЃЉAгыBдкyЃН![]() ЩЯЃЌCгыDдкyЃН|xЉ1|ЩЯЃЌЗжБ№ИљОнКЏЪ§діМѕадХаЖЯЃЛ
ЩЯЃЌCгыDдкyЃН|xЉ1|ЩЯЃЌЗжБ№ИљОнКЏЪ§діМѕадХаЖЯЃЛ
ЃЈ4ЃЉШчЯТЭМЃЌЧѓНтГіжБЯпyЃНЉx+bгыКЏЪ§ЭМЯѓгавЛИіНЛЕуЕФСйНчЕуЃЌДгЖјЕУГіbЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉxЃНЉ3ДњШыyЃН|x+1|ЕУЃЌyЃН2ЃЌ
ЁрmЃН2ЃЌ
АбxЃН3ДњШыyЃН![]() жаЕУЃЌyЃН
жаЕУЃЌyЃН![]() ЃЌ
ЃЌ
ЁрnЃН![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊ2ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМЫљЪОЃК
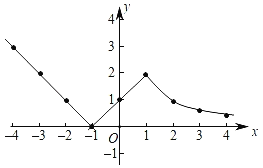
ЃЈ3ЃЉгЩЭМЯѓПЩжЊAгыBдкyЃН![]() ЩЯЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌЫљвдy1ЃОy2ЃЛ
ЩЯЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌЫљвдy1ЃОy2ЃЛ
CгыDдкyЃН|xЉ1|ЩЯЃЌЫљвдx1ЃОx2ЃЛ
ЙЪД№АИЮЊЃОЃЌЃОЃЛ
ЂкЕБyЃН1ЪБЃЌxЁм1ЪБЃЌга1ЃН|x+1|ЃЌ
ЁрxЃН0ЛђxЃНЉ2ЃЌ
ЕБyЃН1ЪБЃЌxЃО1ЪБЃЌга1ЃН![]() ЃЌ
ЃЌ
ЁрxЃН2ЃЌ
ЙЪxЃН0ЛђxЃНЉ2ЛђxЃН2ЃЛ
ЃЈ4ЃЉЁпКЏЪ§НтЮіЪНЮЊЃКyЃН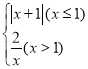 ЃЌЭМЯёШчЯТ
ЃЌЭМЯёШчЯТ

ЕБжБЯпyЃНЉx+bдкЯђгвЦНвЦЕФЙ§ГЬжаЃЌШчЯТЭМЃЌгыКЏЪ§ЕФНЛЕуИіЪ§ЪЧдкБфЛЏЕФЃК
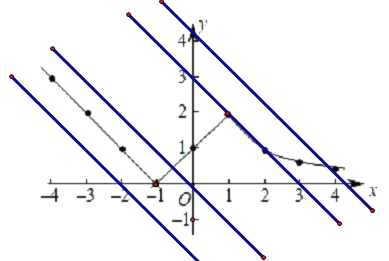
гЩЭМаЮПЩжЊЃЌЕБжБЯпЯђгвЦНвЦЙ§ГЬжаЃЌжБЯпгыКЏЪ§НЛЕуИіЪ§ЮЊЃКЂй0ИіЃЌЂкШЛКѓБфЮЊ1ИіЃЌЂлШЛКѓБфЮЊ2ИіЃЌЂмШЛКѓгжБфЮЊ1Иі
ЮвУЧЗжБ№ЧѓГіЂйЂкЁЂЂкЂлЁЂЂлЂмжЎМфЕФСйНчЕуМДПЩ
гаЭМаЮПЩжЊЃЌЂйЂкжЎМфЕФСйНчЕуЮЊЃКx=Ѓ1
ЮвУЧЧѓГіжБЯпгыКЏЪ§га2ИіНЛЕуЕФЧщПіЃК
СЊСЂНтЮіЪН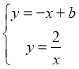 ЕУЃК
ЕУЃК
![]()
ЕБЁїЃО0ЪБЃЌМДжБЯпгыКЏЪ§гаСНИіИіНЛЕу
ЁїЃО![]()
НтЕУbЃО2![]() ЛђbЃМЃ2
ЛђbЃМЃ2![]()
ЙЪЖјЉ1ЃМbЃМ2![]() ЪБЃЌжБЯпгыКЌгагаЧвНігавЛИіНЛЕу
ЪБЃЌжБЯпгыКЌгагаЧвНігавЛИіНЛЕу
ЛЙДцдквЛжжЧщПіЃКШчЯТЭМ
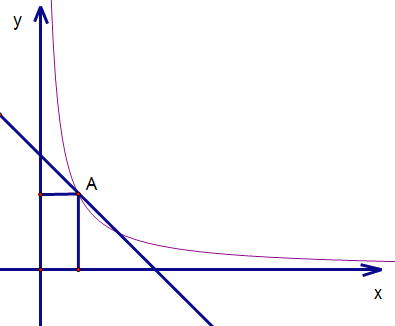
гЩЩЯУцЗжЮіПЩжЊЕБbЃО2![]() ЪБЃЌжБЯпЪЧгыКЏЪ§га2ИіНЛЕуЕФ
ЪБЃЌжБЯпЪЧгыКЏЪ§га2ИіНЛЕуЕФ
ЕЋЪЧЗДБШР§КЏЪ§ЕФШЁжЕЗЖЮЇЮЊxЃО1ЕФВПЗж
ЁрШчЩЯЭМЃЌЗДБШР§КЏЪ§ЪЧЕуA(1ЃЌ2)гвВрЕФВПЗж
ЁрЕБжБЯпy=Ѓx+bДгAЕуМЬајЯђгвЦНвЦЪБЃЌжБЯпгыЗДБШР§КЏЪ§НігавЛИіНЛЕу
НЋЕуAДњШыжБЯпЕУЃК2=Ѓ1+bЃЌНтЕУЃКb=3
ЁрЕБbЃО3ЪБЃЌжБЯпгыКЏЪ§вВНігавЛИіНЛЕу
злЩЯЕУЃЌЉ1ЃМbЃМ2![]() ЛђbЃО3ЃЎ
ЛђbЃО3ЃЎ

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ