题目内容
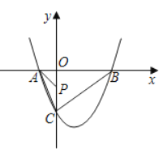
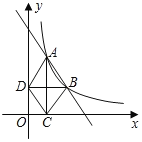
【题目】如图,在直角坐标平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
(x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD,DC,CB.
(1)求反比例函数的解析式;
(2)若△ABD的面积为4,求点B的坐标;
(3)求证:DC![]() AB.
AB.
【答案】(1)y=![]() ;(2)点B的坐标为(3,
;(2)点B的坐标为(3,![]() );(3)证明见解析.
);(3)证明见解析.
【解析】
(1)函数y=![]() 的图象经过A(1,4),可求m=4,则答案可求出,
的图象经过A(1,4),可求m=4,则答案可求出,
(2)由△ABD的面积为4,即![]() a(4-
a(4-![]() )=4,得a=3,则答案可求出;
)=4,得a=3,则答案可求出;
(3)得出![]() =
=![]() 且∠AEB=∠CED,证明△AEB∽△CED,得出∠ABE=∠CDE,则DC∥AB.
且∠AEB=∠CED,证明△AEB∽△CED,得出∠ABE=∠CDE,则DC∥AB.
(1)∵函数y=![]() (x>0,m是常数)图象经过A(1,4),
(x>0,m是常数)图象经过A(1,4),
∴m=4,
∴y=![]()
(2)设BD,AC交于点E,据题意,可得B点的坐标为(a,![]() ),D点的坐标为(0,
),D点的坐标为(0,![]() ),E点的坐标为(1,
),E点的坐标为(1,![]() ),
),

∵a>1,
∴DB=a,AE=4﹣![]() .
.
∵△ABD的面积为4,
∴![]() a(4﹣
a(4﹣![]() )=4,
)=4,
解得:a=3,
∴点B的坐标为(3,![]() );
);
(3)据题意,点C的坐标为(1,0),DE=1.
∵a>1,
∴EC=![]() ,BE=a﹣1,
,BE=a﹣1,
∴![]() =
=![]() =a-1,
=a-1,![]() =
=![]() =a﹣1,
=a﹣1,
∴![]() =
=![]()
∵∠AEB=∠CED,
∴△AEB∽△CED,
∴∠ABE=∠CDE,
∴DC∥AB;

【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数y= 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)列表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | m | 1 | 0 | 1 | 2 | 1 | n |
| … |
其中,m= ,n= .
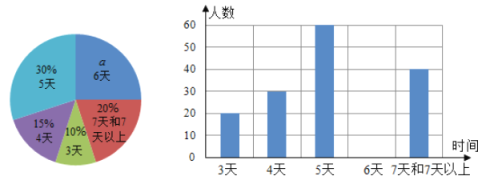
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
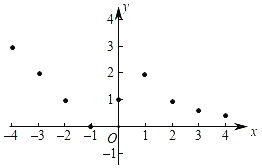
(3)研究函数并结合图象与表格,回答下列问题:
①点A(![]() ,y1),B(5,y2),C(x1,
,y1),B(5,y2),C(x1,![]() ),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=﹣x+b与函数图象有且只有一个交点,请直接写出b的取值范围.
【题目】一般地,对于已知一次函数y1=ax+b,y2=cx+d(其中a,b,c,d为常数,且ac<0),定义一个新函数y=![]() ,称y是y1与y2的算术中项,y是x的算术中项函数.
,称y是y1与y2的算术中项,y是x的算术中项函数.
(1)如:一次函数y1=![]() x﹣4,y2=﹣
x﹣4,y2=﹣![]() x+6,y是x的算术中项函数,即y=
x+6,y是x的算术中项函数,即y=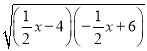 .
.
①自变量x的取值范围是 ,当x= 时,y有最大值;
②根据函数研究的途径与方法,请填写下表,并在图1中描点、连线,画出此函数的大致图象;
x | 8 | 9 | 10 | 12 | 13 | 14 | 16 | 17 | 18 |
y | 0 | 1.2 | 1.6 |
| 2.04 | 2 |
| 1.2 | 0 |
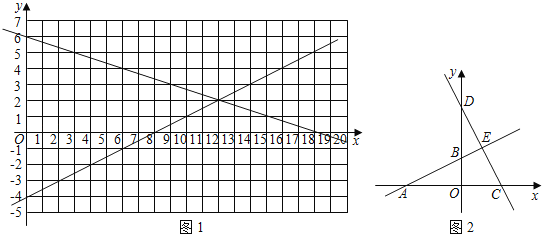
③请写出一条此函数可能有的性质 ;
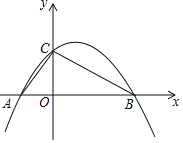
(2)如图2,已知一次函数y1=![]() x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=
x+2,y2=﹣2x+6的图象交于点E,两个函数分别与x轴交于点A,C,与y轴交于点B,D,y是x的算术中项函数,即y=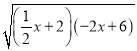 .
.
①判断:点A、C、E是否在此算术中项函数的图象上;
②在平面直角坐标系中是否存在一点,到此算术中项函数图象上所有点的距离相等,如果存在,请求出这个点;如果不存在,请说明理由.