题目内容
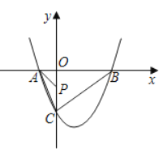
【题目】如图,一次函数![]() 的图像与二次函数
的图像与二次函数![]() 的图像交于
的图像交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴上,点
轴上,点![]() 的横坐标为4.
的横坐标为4.
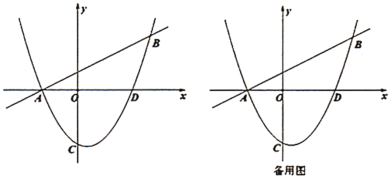
(1)![]() ________,
________,![]() ________;
________;
(2)设二次函数的图像与![]() 轴交于
轴交于![]() 点,与
点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)①若![]() 点在
点在![]() 轴下方二次函数图像上,过
轴下方二次函数图像上,过![]() 点作
点作![]() 轴平行线交直线
轴平行线交直线![]() 于点
于点![]() ,以
,以![]() 点为圆心,
点为圆心,![]() 的长为半径画圆,求
的长为半径画圆,求![]() 在直线
在直线![]() 上截得的弦长的最大值.
上截得的弦长的最大值.
②若∠ABM=∠ACO,则点M的坐标为_________
【答案】(1)![]() ;-3;(2)
;-3;(2)![]() ;(3)①
;(3)①![]() 在直线
在直线![]() 上截得的弦长的最大值等于
上截得的弦长的最大值等于![]() 最大值的2倍,等于
最大值的2倍,等于![]() .②
.②![]()
【解析】
(1)根据条件,易求点A、B的坐标,将其代入二次函数![]() 中,得到关于b,c的方程组求解即可.
中,得到关于b,c的方程组求解即可.
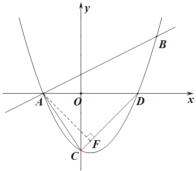
(2)作![]() 于F,易知
于F,易知![]() ,从而得到
,从而得到![]() ,分别用勾股定理和锐角三角函数求出AC,AF的长,在直角三角形ACF中,利用锐角三角函数定义即可求得
,分别用勾股定理和锐角三角函数求出AC,AF的长,在直角三角形ACF中,利用锐角三角函数定义即可求得![]() 的正弦值.
的正弦值.
(3)①作![]() 于
于![]() ,易知
,易知![]() ,故
,故![]() ,得到
,得到![]() ,即
,即![]() ,设
,设![]() ,则
,则![]() 有
有![]() ,转化成二次函数的最值问题即可求得ET的最大值,进而求得在直线上截得的弦长的最大值;
,转化成二次函数的最值问题即可求得ET的最大值,进而求得在直线上截得的弦长的最大值;
②关键是利用勾股定理求得AP=![]() 的值,得到
的值,得到![]() 故点
故点![]() ,再求出直线PB的解析式,进而利用相交法求得点M坐标.
,再求出直线PB的解析式,进而利用相交法求得点M坐标.
解:(1)一次函数解析式![]() ,当x=4是,y=3,∴B(4,3);
,当x=4是,y=3,∴B(4,3);
当y=0时,x=-2,∴A(-2,0),又点A、B在二次函数![]() 的图像上,
的图像上,
∴![]() ,解得
,解得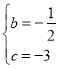 ,
,
故答案为:![]() ,-3
,-3
(2)对于![]() ,令
,令![]() ,则
,则![]() ,∴
,∴![]()
令![]() ,得
,得![]() ,解得:
,解得:![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]()
∴![]()
作![]() 于F,∵
于F,∵![]() ,
,
∴![]() ,
,
∵![]()
∴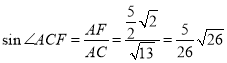 ,
,
∴![]() 的正弦值为
的正弦值为![]() .
.
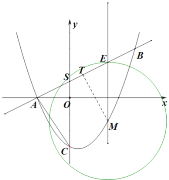
(3)①作![]() 于
于![]() ,
,
设一次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 点,则
点,则![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() 轴,∴
轴,∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]()
∴![]()
∴![]()
∴当![]() 时,
时,![]() 的最大值等于
的最大值等于![]() ,
,
∴![]() 在直线
在直线![]() 上截得的弦长的最大值等于
上截得的弦长的最大值等于![]() 最大值的2倍,等于
最大值的2倍,等于![]() .
.
![]() 如图3,设直线AB交y轴于点H(0,1),直线BM交x轴于点P,过点P作PQ⊥AB于点Q,
如图3,设直线AB交y轴于点H(0,1),直线BM交x轴于点P,过点P作PQ⊥AB于点Q,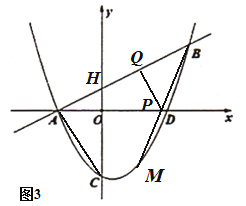
由直线AB的表达式知tan ∠BAO=![]() ,则
,则
在Rt△AQD中,tan∠QAD=tan ∠BAO=![]() =
=![]()
在Rt△AOC中,tan∠ACO=![]() ,
,
又∵∠ABM=∠ACO
tan∠ABM=tan∠ACO=![]() ,
,
设PQ=2x,则QB=3x,AQ=4x,
则 ![]() 解得:
解得: ![]()
又![]() ,
,
![]() 故点
故点 ![]()
由点B,P的坐标得,直线PB的表达式为![]() ,令
,令![]() ①,
①,
联立①②得:![]()
解得:![]() 或
或![]() (与B重合,舍去),将x=
(与B重合,舍去),将x=![]() 代入
代入![]() 得y=
得y=![]()
故点![]() ,
,
故答案为:![]()

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?

【题目】若一个函数当自变量在不同范围内取值时,函数表达式不同,我们称这样的函数为分段函数,下面我们参照学习函数的过程与方法,探究分段函数y= 的图象与性质,探究过程如下,请补充完整.
的图象与性质,探究过程如下,请补充完整.
(1)列表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 3 | m | 1 | 0 | 1 | 2 | 1 | n |
| … |
其中,m= ,n= .
(2)描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图所示,请画出函数的图象.
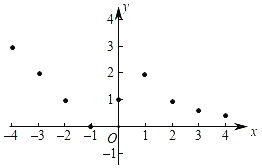
(3)研究函数并结合图象与表格,回答下列问题:
①点A(![]() ,y1),B(5,y2),C(x1,
,y1),B(5,y2),C(x1,![]() ),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
),D(x2,6)在函数图象上,则y1 y2,x1 x2;(填“>”,“=”或“<”)
②当函数值y=1时,求自变量x的值;
(4)若直线y=﹣x+b与函数图象有且只有一个交点,请直接写出b的取值范围.