题目内容
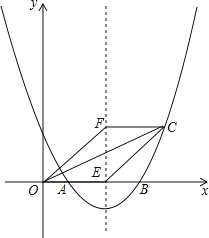
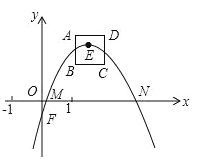
【题目】如图，抛物线l：y=﹣x2+bx+c（b，c为常数），其顶点E在正方形ABCD内或边上，已知点A（1，2），B（1，1），C（2，1）．
（1）直接写出点D的坐标_____________；
（2）若l经过点B，C，求l的解析式；
（3）设l与x轴交于点M，N，当l的顶点E与点D重合时，求线段MN的值；当顶点E在正方形ABCD内或边上时，直接写出线段MN的取值范围；
（4）若l经过正方形ABCD的两个顶点，直接写出所有符合条件的c的值．
【答案】（1）D点的坐标为（2，2）；（2）y=﹣x2+3x﹣1；（3）2≤MN≤
；（4）所有符合条件的c的值为﹣1，1，﹣2．
【解析】试题分析：（1）根据正方形的性质，可得D点的坐标；
（2）根据待定系数法，可得函数解析式；
（3）根据顶点横坐标纵坐标越大，与x轴交点的线段越长，根据顶点横坐标纵坐标越小，与x轴交点的线段越短，可得答案；
（4）根据待定系数法，可得c的值，要分类讨论，以防遗漏．
试题解析：解：（1）由正方形ABCD内或边上，已知点A（1，2），B（1，1），C（2，1），得D点的横坐标等于C点的横坐标，即D点的横坐标为2，D点的纵坐标等于A点的纵坐标，即D点的纵坐标为2，D点的坐标为（2，2）；
（2）把B（1，1）、C（2，1）代入解析式可得：
，解得：
所以二次函数的解析式为y=﹣x2+3x﹣1；
（3）由此时顶点E的坐标为（2，2），得：抛物线解析式为y=﹣（x﹣2）2+2
把y=0代入得：﹣（x﹣2）2+2=0
解得：x1=2﹣
，x2=2+，即N（2+，0），M（2﹣，0），所以MN=2+﹣（2﹣）=2．
点E的坐标为B（1，1），得：抛物线解析式为y=﹣（x﹣1）2+1
把y=0代入得：﹣（x﹣1）2+1=0
解得：x1=0，x2=2，即N（2，0），M（0，0），所以MN=2﹣0=2．
点E在线段AD上时，MN最大，点E在线段BC上时，MN最小；
当顶点E在正方形ABCD内或边上时，2≤MN≤2；
（4）当l经过点B，C时，二次函数的解析式为y=﹣x2+3x﹣1，c=﹣1；
当l经过点A、D时，E点不在正方形ABCD内或边上，故排除；
当l经过点B、D时，
，解得：
，即c=﹣2；
当l经过点A、C时，
，解得
，即c=1；
综上所述：l经过正方形ABCD的两个顶点，所有符合条件的c的值为﹣1，1，﹣2．
