Question

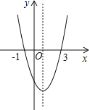
【题目】如图，抛物线y＝ax2+bx+c交x轴分别于点A（﹣3，0），B（1，0），交y轴正半轴于点D，抛物线顶点为C．下列结论：①2a﹣b＝0；②a+b+c＝0；③a﹣b＞am2+bm；④当△ABC是等腰直角三角形时，a＝﹣0.5；⑤若D（0，3），则抛物线的对称轴直线x＝﹣1上的动点P与B、D两点围成的△PBD周长最小值为．其中，正确的个数为_____．

Answer 1

【答案】4

【解析】

利用待定系数法，二次函数的性质，等腰直角三角形的性质，两点之间线段最短一一判断即可．

解：把A（﹣3，0），B（1，0）代入y＝ax2+bx+c得到 ，

消去c得到2a﹣b＝0，故①②正确，

∵抛物线的对称轴直线x=＝﹣1，开口向下，

∴x＝﹣1时，y有最大值，最大值＝a﹣b+c，

∵m≠﹣1，

∴a﹣b+c＞am2+bm+c，

∴a﹣b＞am2+bm，故③正确，

当△ABC是等腰直角三角形时，则CE=BE=2，

∴C（﹣1，2），

可以假设抛物线的解析式为y＝a（x+1）2+2，把（1，0）代入得到a＝﹣0.5，故④正确，

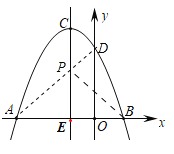
如图，连接AD交抛物线的对称轴于P，连接PB，此时△BDP的周长最小，最小值＝PD+PB+BD＝PD+PA+BD＝AD+BD，

∵AD＝＝3，BD＝＝，

∴△△PBD周长最小值为3+，故⑤错误．

故答案为4．