题目内容
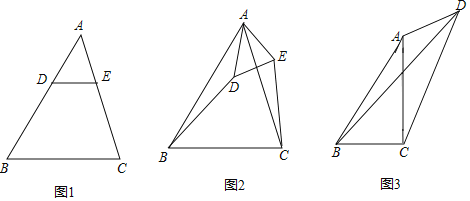
【题目】(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=![]() ,则
,则![]() 的值是 ;
的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,![]() 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
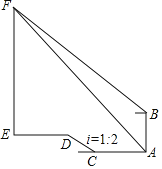
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=![]() ,当CD=6,AD=3时,请直接写出线段BD的长度.
,当CD=6,AD=3时,请直接写出线段BD的长度.
【答案】(1)![]() ;(2)
;(2)![]() 的值不变化,值为
的值不变化,值为![]() ,理由见解析;(3)
,理由见解析;(3)![]()
![]()
【解析】
(1)由平行线分线段成比例定理即可得出答案;
(2)证明△ABD∽△ACE,得出![]() =
=![]() =
=![]()
(3)作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,则DM=CN,DN=MC,由三角函数定义得出![]() =
=![]() ,
,![]() =
=![]() ,得出
,得出![]() =
=![]() ,求出AE=
,求出AE=![]() AD=
AD=![]() ,DE=
,DE=![]() AE=
AE=![]() ,得出CE=CD﹣DE=
,得出CE=CD﹣DE=![]() ,由勾股定理得出AC=
,由勾股定理得出AC=![]() =
=![]() ,得出BC=
,得出BC=![]() AC=
AC=![]()
,由面积法求出CN=DM=![]() ,得出BN=BC+CN=
,得出BN=BC+CN=![]() ,由勾股定理得出AM=
,由勾股定理得出AM=![]() =
=![]() ,得出DN=MC=AM+AC=
,得出DN=MC=AM+AC=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
(1)∵DE∥BC,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
故答案为:![]() ;
;
(2)![]() 的值不变化,值为
的值不变化,值为![]() ;理由如下:
;理由如下:
由(1)得:DE∥B,
∴△ADE∽△ABC,
∴![]() =
=![]() ,
,
由旋转的性质得:∠BAD=∠CAE,
∴△ABD∽△ACE,
∴![]() =
=![]() =
=![]() ;
;
(3)作AE⊥CD于E,DM⊥AC于M,DN⊥BC于N,如图3所示:
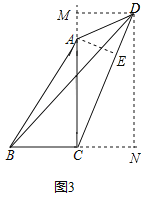
则四边形DMCN是矩形,
∴DM=CN,DN=MC,
∵∠BAC=∠ADC=θ,且tanθ=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴AE=![]() AD=
AD=![]() ×3=
×3=![]() ,DE=
,DE=![]() AE=
AE=![]() ,
,
∴CE=CD﹣DE=6﹣![]() =
=![]() ,
,
∴AC=![]() =
=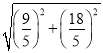 =
=![]()
∴BC=![]() AC=
AC=![]() ,
,
∵△ACD的面积=![]() AC×DM=
AC×DM=![]() CD×AE,
CD×AE,
∴CN=DM=![]() =
=![]() ,
,
∴BN=BC+CN=![]() ,AM=
,AM=![]() =
=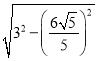 =
=![]() ,
,
∴DN=MC=AM+AC=![]() ,
,
∴BD=![]() =
=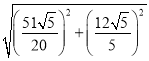 =
=![]()
![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛. 赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:
分数段 (分数为x分) | 频数 | 百分比 |
60≤x<70 | 8 | 20% |
70≤x<80 | a | 30% |
80≤x<90 | 16 | b% |
90≤x<100 | 4 | 10% |
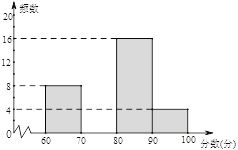
(1)表中的a= ,b= ;
(2)请补全频数分布直方图;
(3)若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应的圆心角的度数是 ;
(4)竞赛成绩不低于90分的4名同学中正好有2名男同学,2名女同学.学校从这4名同学中随机抽取2名同学接受电视台记者采访,请用列表或画树状图的方法求正好抽到一名男同学和一名女同学的概率.