题目内容
【题目】如图,在
中，
,以边
的中点
为圆心,作半圆与
相切，点
分别是边
和半圆上的动点,连接
,则长的最大值与最小值的和是（ ）
A.
B.
C.
D.
【答案】C
【解析】
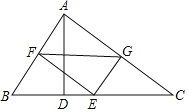
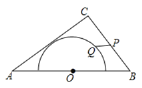
如图，设⊙O与AC相切于点E，连接OE，作OP1⊥BC垂足为P1交⊙O于Q1，此时垂线段OP1最短，P1Q1最小值为OP1-OQ1，求出OP1，如图当Q2在AB边上时，P2与B重合时，P2Q2最大值=5+3=8，由此不难解决问题．
解：如图，设⊙O与AC相切于点E，连接OE，作OP1⊥BC垂足为P1交⊙O于Q1，
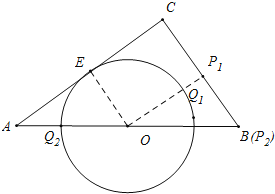
此时垂线段OP1最短，P1Q1最小值为OP1-OQ1，
∵AB=10，AC=8，BC=6，
∴AB2=AC2+BC2，
∴∠C=90°，
∵∠OP1B=90°，
∴OP1∥AC
∵AO=OB，\
∴P1C=P1B，
∴OP1=
AC=4，
∴P1Q1最小值为OP1-OQ1=1，
如图，当Q2在AB边上时，P2与B重合时，P2Q2经过圆心，经过圆心的弦最长，
P2Q2最大值=5+3=8，
∴PQ长的最大值与最小值的和是9．
故选：C．
练习册系列答案
相关题目
【题目】在不透明的袋子中有四张标有数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下：
小华列出表格如下：
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是：随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为 ；
（3）规定两次抽到的数字之和为奇数的获胜，你认为淮获胜的可能性大？为什么？
