题目内容
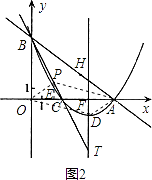
【题目】已知:如图,在平面直角坐标系xOy中,直线y= ![]() x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
(1)直接写出点C的坐标,并求过A、B、C三点的抛物线的解析式;
(2)若(1)中抛物线的顶点为D,在直线BC上是否存在点P,使得四边形ODAP为平行四边形?若存在,求出点P的坐标;若不存在,说明理由;
(3)若把(1)中的抛物线向左平移3.5个单位,则图象与x轴交于F、N(点F在点N的左侧)两点,交y轴于E点,则在此抛物线的对称轴上是否存在一点Q,使点Q到E、N两点的距离之差最大?若存在,请求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:连接CH,
由轴对称得CH⊥AB,BH=BO,CH=CO
∴在△CHA中由勾股定理,得
AC2=CH2+AH2
∵直线y= ![]() x+6与x轴、y轴的交点分别为A、B两点,
x+6与x轴、y轴的交点分别为A、B两点,
∴当x=0时,y=6,当y=0时,x=8
∴B(0,6),A(8,0)
∴OB=6,OA=8,
在Rt△AOB中,由勾股定理,得
AB=10
设C(a,0),∴OC=a
∴CH=a,AH=4,AC=8﹣a,在Rt△AHC中,
由勾股定理,得
(8﹣a)2=a2+42解得
a=3
C(3,0)
设抛物线的解析式为:y=ax2+bx+c,由题意,得
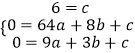
解得: 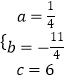
∴抛物线的解析式为:y= ![]() x2
x2 ![]() +6,
+6,
∴y= ![]()
![]()
![]()

(2)
解:由(1)的结论,得
D( ![]() ,﹣
,﹣ ![]() )
)
∴DF= ![]() ,
,
设BC的解析式为:y=kx+b,则有
![]()
解得: ![]()
直线BC的解析式为:y=﹣2x+6
设存在点P使四边形ODAP是平行四边形,P(m,n)
作PE⊥OA于E,HD交OA于F.
∴∠PEO=∠AFD=90°,PO=DA,PO∥DA
∴∠POE=∠DAF
∴△OPE≌△ADF
∴PE=DF=n= ![]() ,
,
∴ ![]() =﹣2x+6
=﹣2x+6
∴ ![]()
P( ![]() ,
, ![]() )
)
当x= ![]() 时,
时,
y=﹣2× ![]() +6=1≠
+6=1≠ ![]()
∴点P不再直线BC上,即直线BC上不存在满足条件的点P
(3)
解:由题意得,平移后的解析式为:
y= ![]() (x﹣2)2
(x﹣2)2 ![]()
∴对称轴为:x=2,
当x=0时,y=﹣ ![]()
当y=0时,0= ![]() (x﹣2)2
(x﹣2)2 ![]()
解得:x1= ![]() ;x2=
;x2= ![]()
∵F在N的左边
F( ![]() ,0),E(0,﹣
,0),E(0,﹣ ![]() ),N(
),N( ![]() ,0)
,0)
连接EF交x=2于Q,设EF的解析式为:y=kx+b,则有

解得: 
∴EF的解析式为:y=﹣ ![]() x﹣
x﹣ ![]()
∴ 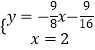
解得:
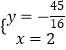
∴Q(2,﹣ ![]() ).
).
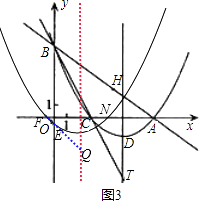
【解析】(1)根据轴对称和角平分线的性质以及勾股定理可以求出OC的长度,从而求出点C的坐标.再根据直线的解析式求出A、B的坐标,最后利用待定系数法就可以求出抛物线的解析式.(2)根据(1)的解析式可以转化为顶点式而求出顶点坐标D,利用B、C的坐标求出BC的解析式,假设在直线BC上存在满足条件的点P,利用平行四边形的性质和三角形全等的性质求出点P的坐标,得到点P不在直线BC上,而得出结论.(3)平移后根据(1)的解析式可以得到平移后的解析式,顶点坐标及对称轴,可以求出与坐标轴的交点F、N、E的坐标,连接EF,根据E、F的坐标求出其解析式,求出EF与对称轴的交点,就是Q点.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案





