Question

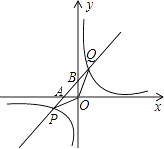
【题目】如图1所示，E为矩形ABCD的边AD上一点，动点P、Q同时从点B出发，点P以1cm/秒的速度沿折线BE﹣ED﹣DC运动到点C时停止，点Q以2cm/秒的速度沿BC运动到点C时停止．设P、Q同时出发t秒时，△BPQ的面积为ycm2 ． 已知y与t的函数关系图象如图2；（其中曲线OG为抛物线的一部分，其余各部分均为线段），则下列结论：
①当0＜t≤5时，y= t2；②当t=6秒时，△ABE≌△PQB；③cos∠CBE= ；④当t= 秒时，△ABE∽△QBP；
其中正确的是（ ）

A.①②
B.①③④
C.③④
D.①②④

Answer 1

【答案】D
【解析】解：根据图（2）可得，点Q到达点E时时间是5秒，点P到达点E时间为10秒，

∵点P、Q的运动的速度分别是1cm/秒、2cm/秒
∴BC=BE=10，
∴AD=BC=10．
又∵从M到N的变化是4，
∴ED=4，
∴AE=AD﹣ED=10﹣4=6．
∵AD∥BC，
∴∠1=∠2，
∴cos∠1=cos∠2= = = ．
故③错误；
如图1，过点P作PF⊥BC于点F，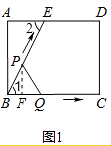

∵AD∥BC，
∴∠1=∠2，
∴sin∠1=sin∠2= = = ，
∴PF=PBsin∠1= t，
∴当0＜t≤5时，y= BQPF= ×2t× t= t2 ， 故①正确；
如图3，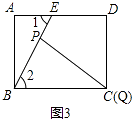

当t=6秒时，点P在BE上，点Q静止于点C处．
在△ABE与△PQB中， ，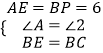
∴△ABE≌△PQB（SAS）．
故②正确；
如图4，

当t= 秒时，点P在CD上，此时，PD= ﹣BE﹣ED= ﹣10﹣4= ，
PQ=CD﹣PD=8﹣ = ，
∵ = = ， = = ，
∴ =
又∵∠A=∠Q=90°，
∴△ABE∽△QBP，故④正确．
综上所述，正确的结论是①②④．
故选D．
【考点精析】通过灵活运用函数的图象，掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值即可以解答此题．