Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8cm，BC=6cm，点M是边AB的中点，连结CM，点P从点C出发，以1cm/s的速度沿CB运动到点B停止，以PC为边作正方形PCDE，点D落在线段AC上．设点P的运动时间为t（s）．
（1）当t=时，点E落在△MBC的边上；
（2）以E为圆心，1cm为半径作圆E，则当t=时，圆E与直线AB或直线CM相切．

Answer 1

【答案】
（1）
（2） ； ；5
【解析】解：（1）如图1，∵四边形PCDE是正方形，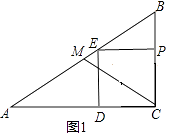
∴DP∥AC，
∴ = ，
即 = ，
解得t= ；（2）如图2，当点E在△ABC的内部时，圆E与直线AB相切，EF⊥
AB，且EF=1时，

连接AE、BE、CE，
∵∠ACB=90°，AC=8，BC=6，
∴AB=10，
×AB×EF+ + ×BC×EP= ×AC×BC，
×10×1+ ×8×t+ ×6×t= ×8×6，
解得t= ；
如图3，当点E在△ABC的外部时，圆E与直线AB相切，EG⊥AB，且EG=1时，

∵∠EGH=∠BPH，∠EHG=∠BHP，
∴∠GEH=∠PBH，
∴cos∠GEH=cos∠ABC= = ，又EG=1，
∴EH= ，
∵ = ，∴HP= ，
则 + =t，
解得t= ；
如图4，当圆E与直线CM相切时，EN=1，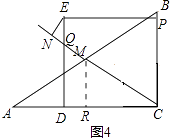

作MR∥BC，则MR= BC=3，CR= AC=4，
∵点M是边AB的中点，
∴CM= AB=5，
tan∠ACM= = ，
∴ = ，CD=t，
则QD= t，EQ= t，
∵∠NEQ=∠ACM，
∴ = = ，
解得t=5．