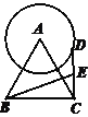题目内容
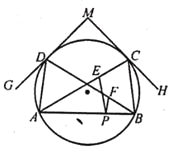
【题目】如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A. 4B. 2 ![]() C. 4
C. 4 ![]() D. 不确定
D. 不确定
【答案】A
【解析】
易证:AD=BC=4.通过证明△AEP∽△ACB,△BFP∽△BDA.从而求出PE+PF=4,因而PE+PF是定值.
解:当∠ADG=∠BCH=30°时,PE+PF是定值,理由如下:
连结OA、OB、OC、OD,如图:
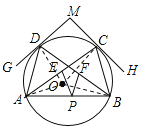
∵DG与 ⊙O 相切,
∴∠GDA=∠ABD,
∵∠ADG=30°,
∴∠ABD=30°,
∴∠AOD=2∠ABD=60°,
∵OA=OD,
∴△AOD为等边三角形,
∴AD=OA=4,
同理可得:BC=4,
∵PE∥BC,PF∥AD,
∴△AEP∽△ACB,△BFP∽△BDA,
![]() ,
,
![]() ,
,
![]() ,
,
∴PE+PF=4,
∴当∠ADG=∠BCH=30°时,PE+PF=4.
故答案为:A.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?