题目内容
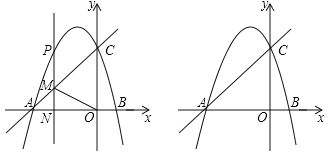
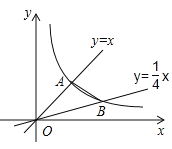
【题目】如图,直线y=x与直线![]() 分别与双曲线
分别与双曲线![]() 交于A、B两点,S△OAB=3,则k=________
交于A、B两点,S△OAB=3,则k=________
.
【答案】4
【解析】
作AD⊥x轴于D,BC⊥x轴于C,根据点A、B分别在直线y=x和直线y=![]() x上,且它们都在y=
x上,且它们都在y=![]() 上,则设点A的横坐标为a,则纵坐标为y=a,且k=aa=a2,a=
上,则设点A的横坐标为a,则纵坐标为y=a,且k=aa=a2,a=![]() ;点B的横坐标为b,则纵坐标为y=
;点B的横坐标为b,则纵坐标为y=![]() b,且k=b
b,且k=b![]() b=
b=![]() b2,即b=2
b2,即b=2![]() ,由于S△AOD+S梯形ABCD=S△AOB+S△BOC,根据k的几何意义得到S△AOD=S△BOC=
,由于S△AOD+S梯形ABCD=S△AOB+S△BOC,根据k的几何意义得到S△AOD=S△BOC=![]() k,于是S梯形ABCD=3,
k,于是S梯形ABCD=3,
即![]() (
(![]() b+a)(b-a)=3,展开后得到ab=8,然后把a=
b+a)(b-a)=3,展开后得到ab=8,然后把a=![]() ,b=2
,b=2![]() 代入计算即可得到k的值.
代入计算即可得到k的值.
解:作AD⊥x轴于D,BC⊥x轴于C,如图,

设点A的横坐标为a,则纵坐标为y=a,且k=aa=a2,a=![]() ;点B的横坐标为b,则纵坐标为y=
;点B的横坐标为b,则纵坐标为y=![]() b,且k=b
b,且k=b![]() b=
b=![]() b2,即b=2
b2,即b=2![]() ,
,
∵S△AOD+S梯形ABCD=S△AOB+S△BOC,
而S△AOD=S△BOC=![]() k,S△OAB=3,
k,S△OAB=3,
∴S梯形ABCD=3,
∴![]() (
(![]() b+a)(b-a)=3,
b+a)(b-a)=3,
∴![]() b2-a
b2-a![]() b+ab-a2=6,
b+ab-a2=6,
∴k+![]() ab-k=6,
ab-k=6,
∴ab=8,
∵a=![]() ,b=2
,b=2![]()
![]() ,
,
∴k=2.
故答案为2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目