题目内容
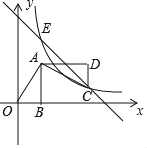
【题目】正△ABC的边长为4,⊙A的半径为2,D是⊙A上动点,E为CD中点,则BE的最大值为____.
【答案】![]()
【解析】
延长CB到点F,使FB=BC=4,连接AF,过点A作AH⊥FC于点H,找出点F与⊙A上距离最近、最远的点,即可得出DF的取值范围,从而求出最大值,再根据BE是△CDF的中位线即可解答.
解:如图:延长CB到点F,使FB=BC=4,连接AF,过点A作AH⊥FC于点H,
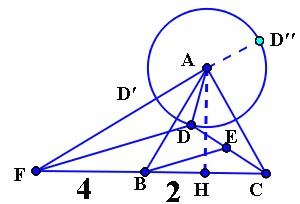
又∵正△ABC的边长为4,
∴AH=2![]() ,BH=2,
,BH=2,
在Rt△AFH中,由勾股定理易得AF=![]() =4
=4![]()
∵E为CD中点,
∴BE∥DF,BE=![]() DF
DF
当点D与D′重合时,FD最小此时FD=4![]() -2;当点D与D′′重合时,FD最大,此时FD=4
-2;当点D与D′′重合时,FD最大,此时FD=4![]() +2,即AF-AD≤FD≤AF+AD
+2,即AF-AD≤FD≤AF+AD
∴BE的最大值为![]() ( 4
( 4![]() +2)=
+2)=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目