题目内容
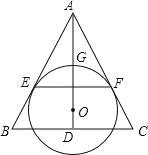
【题目】如图,已知:在矩形ABCD中,O为AC的中点,直线l经过点B,且直线l绕着点B旋转,AM⊥l于点M,CN⊥l于点N,连接OM,ON
(1)当直线l经过点D时,如图1,则OM、ON的数量关系为 ;
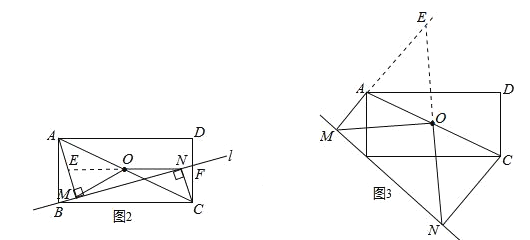
(2)当直线l与线段CD交于点F时,如图2(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由;
(3)当直线l与线段DC的延长线交于点P时,请在图3中作出符合条件的图形,并判断(1)中的结论是否仍然成立?不必说明理由.

【答案】(1)OM=ON;(2)结论仍然成立.(3)结论仍然成立.
【解析】
试题分析:(1)OM=ON;易证△AOM≌△CON,所以OM=ON;
(2)结论仍然成立.如答图2,作辅助线,证明△AEO≌△CNO,得点O为Rt△MEN斜边上的中点,所以OM=ON结论成立;
(3)结论仍然成立.与(2)同理.
试题解析:(1)OM=ON;如题图1,
∵O为AC的中点,
∴OA=OB,
∵AM⊥l于点M,CN⊥l于点N,
∴∠AMO=∠CNO=90°,
在△AMO和△CNO中,
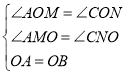 ,
,
∴△AMO≌△CNO(AAS)
∴OM=ON;
(2)(1)中的结论仍然成立.理由如下:
如答图2,延长NO,交AM于点E,
∵AM⊥l于点M,CN⊥l于点N,
∴AM∥CN,
∴∠OAE=∠OCN.
∵矩形ABCD,点O为对角线AC中点,
∴OA=OC.
在△AEO和△CNO中,
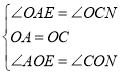
∴△AEO≌△CNO(ASA)
∴OE=ON,
∵Rt△MEN,点O为EN的中点
∴OM=ON(直角三角形斜边上的中线等于斜边的一半).
(3)(1)中的结论仍然成立.理由如下:
如答图3,延长NO,交MA的延长线于点E.
与(2)同理,可以证明OM=ON.

 名校课堂系列答案
名校课堂系列答案【题目】甲、乙、丙、丁四位同学五次100米跑成绩统计如下表.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加县运动会,那么应选( )
甲 | 乙 | 丙 | 丁 | |
平均数(秒) | 16 | 15 | 15 | 16 |
方差 | 30 | 30 | 35 | 42 |
A. 甲B. 乙C. 丙D. 丁