题目内容
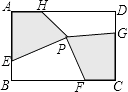
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点F在边AC上,并且CF=1,点E为边BC上的动点,将△CEF沿直线EF翻折,点C落在点P处,则点P到边AB距离的最小值是 . 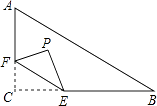
【答案】![]()
【解析】解:如图,延长FP交AB于M, 
当FP⊥AB时,点P到AB的距离最小,
∵∠C=90°,AC=3,BC=4,
∴AB= ![]() =5,
=5,
∵∠A=∠A,∠AMF=∠C=90°,
∴△AFM∽△ABC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得,FM= ![]() ,
,
由折叠的性质可知,FP=FC=1,
∴PM= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和翻折变换(折叠问题),需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目