题目内容
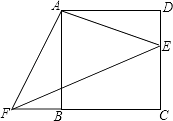
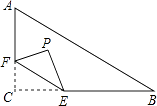
【题目】图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为25°,长为2.1米的真空管AB与水平线AD的夹角为40°,安装热水器的铁架水平横管BC长0.2米,求 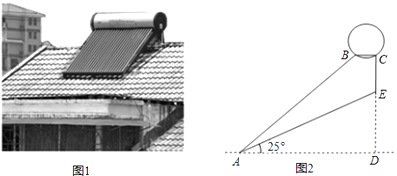
(1)真空管上端B到AD的距离(结果精确到0.01米);
(2)铁架垂直管CE的长(结果精确到0.01米).
【答案】
(1)解:过B作BF⊥AD于F.
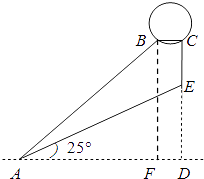
在Rt△ABF中,
∵sin∠BAF= ![]() ,
,
∴BF=ABsin∠BAF=2.1sin40°≈1.350.
∴真空管上端B到AD的距离约为1.35米
(2)解:在Rt△ABF中,
∵cos∠BAF= ![]() ,
,
∴AF=ABcos∠BAF=2.1cos40°≈1.609.
∵BF⊥AD,CD⊥AD,又BC∥FD,
∴四边形BFDC是矩形.
∴BF=CD,BC=FD.
在Rt△EAD中,
∵tan∠EAD= ![]() ,
,
∴ED=ADtan∠EAD=1.809tan25°≈0.844.
∴CE=CD﹣ED=1.350﹣0.844=0.506≈0.51
∴安装铁架上垂直管CE的长约为0.51米.
【解析】(1)过B作BF⊥AD于F.构建Rt△ABF中,根据三角函数的定义与三角函数值即可求出答案.(2)根据BF的长可求出AF的长,再判定出四边形BFDC是矩形,可求出AD与ED的长,再用CD的长减去ED的长即可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目