题目内容
【题目】如图,矩形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,点P在矩形ABCD内.若AB=4cm,BC=6cm,AE=CG=3cm,BF=DH=4cm,四边形AEPH的面积为5cm2 , 则四边形PFCG的面积为cm2 . 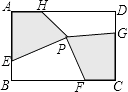
【答案】8
【解析】解:连接AP,CP,设△AHP在AH边上的高为x,△AEP在AE边上的高为y. 则△CFP在CF边上的高为4﹣x,△CGP在CG边上的高为6﹣y.
∵AH=CF=2cm,AE=CG=3cm,
∴S四边形AEPH=S△AHP+S△AEP .
=AH×x× ![]() +AE×y×
+AE×y× ![]()
=2x× ![]() +3y×
+3y× ![]() =5cm2
=5cm2
2x+3y=10
S四边形PFCG=S△CGP+S△CFP=CF×(4﹣x)× ![]() +CG×(6﹣y)×
+CG×(6﹣y)× ![]()
=2(4﹣x)× ![]() +3(6﹣y)×
+3(6﹣y)× ![]()
=(26﹣2x﹣3y)× ![]()
=(26﹣10)× ![]()
=8cm2 .
所以答案是8.
【考点精析】利用矩形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目