题目内容
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A,C分别在y轴,x轴上,∠ACB=90°,OA= ![]() ,抛物线y=ax2﹣ax﹣a经过点B(2,
,抛物线y=ax2﹣ax﹣a经过点B(2, ![]() ),与y轴交于点D.
),与y轴交于点D.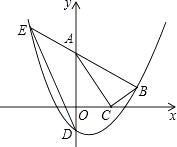
(1)求抛物线的表达式;
(2)点B关于直线AC的对称点是否在抛物线上?请说明理由;
(3)延长BA交抛物线于点E,连接ED,试说明ED∥AC的理由.
【答案】
(1)
解:把点B的坐标代入抛物线的表达式,得 ![]() =a×22﹣2a﹣a,
=a×22﹣2a﹣a,
解得a= ![]() ,
,
∴抛物线的表达式为y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() .
.
(2)
解:连接CD,过点B作BF⊥x轴于点F,则∠BCF+∠CBF=90°
∵∠ACB=90°,
∴∠ACO+∠BCF=90°,
∴∠ACO=∠CBF,
∵∠AOC=∠CFB=90°,
∴△AOC∽△CFB,
∴ ![]() =
= ![]() ,
,
设OC=m,则CF=2﹣m,则有 ![]() =
= ![]() ,
,
解得m1=m2=1,
∴OC=CF=1,
当x=0时,y=﹣ ![]() ,
,
∴OD= ![]() ,
,
∴BF=OD,
∵∠DOC=∠BFC=90°,
∴△OCD≌△FCB,
∴DC=CB,∠OCD=∠FCB,
∴点B、C、D在同一直线上,
∴点B与点D关于直线AC对称,
∴点B关于直线AC的对称点在抛物线上.
(3)
解:过点E作EG⊥y轴于点G,设直线AB的表达式为y=kx+b,则 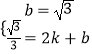 ,
,
解得k=﹣ ![]() ,
,
∴y=﹣ ![]() x+
x+ ![]() ,代入抛物线的表达式﹣
,代入抛物线的表达式﹣ ![]() x+
x+ ![]() =
= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() .
.
解得x=2或x=﹣2,
当x=﹣2时y=﹣ ![]() x+
x+ ![]() =﹣
=﹣ ![]() ×(﹣2)+
×(﹣2)+ ![]() =
= ![]() ,
,
∴点E的坐标为(﹣2, ![]() ),
),
∵tan∠EDG= ![]() =
= ![]() =
= ![]() ,
,
∴∠EDG=30°
∵tan∠OAC= ![]() =
= ![]() =
= ![]() ,
,
∴∠OAC=30°,
∴∠OAC=∠EDG,
∴ED∥AC.
【解析】(1)把点B的坐标代入抛物线的表达式即可求得.(2)通过△AOC∽△CFB求得OC的值,通过△OCD≌△FCB得出DC=CB,∠OCD=∠FCB,然后得出结论.(3)设直线AB的表达式为y=kx+b,求得与抛物线的交点E的坐标,然后通过解三角函数求得结果.
【考点精析】关于本题考查的二次函数的图象和二次函数的性质,需要了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能得出正确答案.