题目内容
(本小题满分8分)
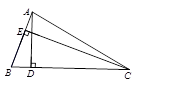
已知,在△ABC中,∠BAC=90°,AB=AC,BC= ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
小题1:(1)请在图①中找出两对相似但不全等的三角形,写在横线上 , ;
小题2:(2)设BE=m,CD=n,求m与n的函数关系式,并写出自 变量n的取值范围;
变量n的取值范围;
小题3:(3)如图②,当BE=CD时,求DE的长;
小题4:(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.
已知,在△ABC中,∠BAC=90°,AB=AC,BC=
 ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.小题1:(1)请在图①中找出两对相似但不全等的三角形,写在横线上 , ;
小题2:(2)设BE=m,CD=n,求m与n的函数关系式,并写出自
 变量n的取值范围;
变量n的取值范围;小题3:(3)如图②,当BE=CD时,求DE的长;
小题4:(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.

小题1:解:(1)△ADE∽△BAE,△ADE∽△CDA,△BAE∽△CDA;(写出任意两对即可)
小题2:(2)∵∠BAC=90°,AB=AC,BC=
 ,
,由(1)知△BAE∽△CDA,
∴
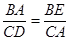 .
.∴
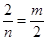 . ∴
. ∴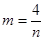 (
(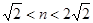 )
)小题3:(3)由(2)只BE·CD=4,
∴BE=CD=2.
∴BD=BC-CD=
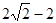 .
.∴DE=BE-BD=
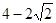
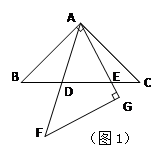
小题4:(4)如图,依题意,可以将△AEC绕点A顺时针旋转90°至△AFB的位置,
则FB=CE,AF=AE,∠1=∠2,
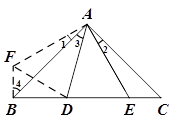 ∴∠FBD=90°.
∴∠FBD=90°.∴
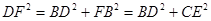 . ……………6分
. ……………6分∵∠3+∠1=∠3+∠2=45°,
∴∠FAD=∠DAE.
又∵AD=AD,AF=AE,
∴△AFD≌△AED.
∴DE=DF. ………………………………………………………………………7分
∴
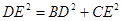
略

练习册系列答案
相关题目
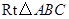 中,
中,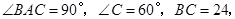 点
点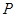 是
是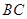 边上的动点(点
边上的动点(点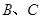 不重合),过动点
不重合),过动点 交
交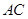 于点
于点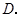
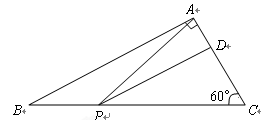
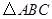 与
与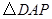 相似,则
相似,则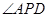 是多少度?
是多少度?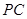 等于多少时,
等于多少时,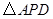 的面积最大?最大面积是多少?
的面积最大?最大面积是多少? 为直径的圆相外切,
为直径的圆相外切,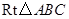 ,
,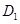 是斜边
是斜边 的中点,过
的中点,过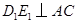 于
于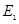 ,连结
,连结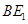 交
交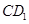 于
于 ;过
;过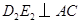 于
于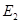 ,连结
,连结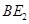 交
交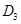 ;过
;过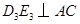 于
于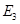 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点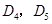 ,…,
,…,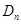 ,分别记
,分别记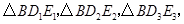 …,
…,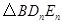 的面积为
的面积为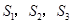 ,…
,…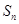 .则( )
.则( )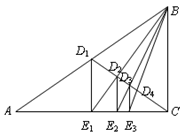
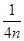

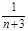
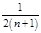
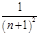
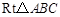 中,
中,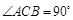 ,
,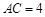 ,
,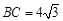 ,以
,以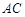 为直径的⊙O交
为直径的⊙O交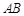 于点
于点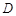 ,点
,点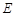 是
是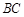 的中点,OB,DE相交于点F。
的中点,OB,DE相交于点F。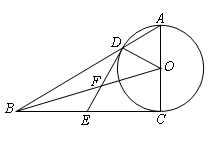
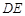 是⊙O的切线;
是⊙O的切线; 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作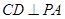 ,垂足为D.
,垂足为D.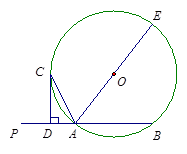
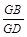 的值.
的值.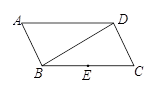
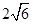 ,sin∠BCE=
,sin∠BCE=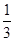 . 求CE的长.
. 求CE的长.