Question

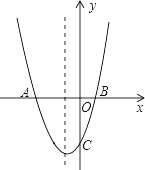
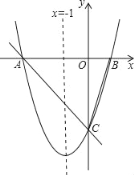
【题目】如图，对称轴为直线x＝﹣1的抛物线y＝ax2+bx+c（a≠0）与x轴相交于A，B两点．

（1）若点A的坐标为（﹣4，0），求点B的坐标．

（2）若已知a＝1，点A的坐标为（﹣3，0），C为抛物线与y轴的交点．

①若点P在抛物线上，且S△POC＝4S△BOC，求点P的坐标；

②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值．

Answer 1

【答案】（1）B（2，0）；（2）①P（4，21），（﹣4，5）；②当m＝﹣时，QD的最大值为．

【解析】

（1）根据抛物线与x轴的两个交点关于对称轴对称，可求B点坐标；
（2）①根据题意可求抛物线解析式，可求△BOC的面积，根据S△POC=4S△BOC，可求P点坐标；
③求出直线AC解析式，设点Q（m，-m-3）（-3≤m≤0），则点D（m，m2+2m-3），根据二次函数的最值求法，可求QD的最大值．

（1）∵对称轴是直线x＝﹣1，点A的坐标为（﹣4，0），且A，B关于对称轴对称，

∴B（2，0）；

（2）①∵对称轴是直线x＝﹣1，点A的坐标为（﹣3，0），且A，B关于对称轴对称，

∴B（1，0），即OB＝1，

∵a＝1，

∴抛物线解析式y＝（x﹣1）（x+3）＝x2+2x﹣3；

当x＝0时，y＝﹣3，

∴点C（0，﹣3），即OC＝3，

∴S△BOC＝OB×OC＝，

设P（x，x2+2x﹣3），

∴S△POC＝×3×|x|，

∵S△POC＝4S△BOC，

∴|x|＝4×，

∴x＝±4，

∴P（4，21），（﹣4，5）；

②∵点A（﹣3，0），点C（0，﹣3），

∴直线AC解析式y＝﹣x﹣3，

∴设点Q（m，﹣m﹣3）（﹣3≤m≤0），

则点D（m，m2+2m﹣3），

∴QD＝﹣m﹣3﹣（m2+2m﹣3）＝﹣（m+）2+，

∴当m＝﹣时，QD的最大值为．