Question

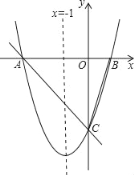
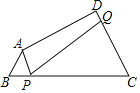
【题目】已知：如图，在Rt△ABC中，BC＝AC＝2，点M是AC边上一动点，连接BM，以CM为直径的⊙O交BM于N，则线段AN的最小值为___．

Answer 1

【答案】﹣1

【解析】

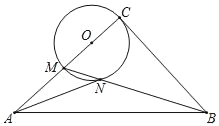
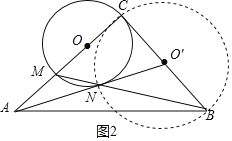
如图1，连接CN，根据CM是⊙O的直径，得到∠CNM=90°，根据邻补角的定义得到∠CNB=90°，根据圆周角定理得到点N在以BC为直径的⊙O'上，推出当点O'、N、A共线时，AN最小，如图2，根据勾股定理即可得到结论．

如图1，连接CN．

∵CM是⊙O的直径，

∴∠CNM=90°，

∴∠CNB=90°，

∴点N在以BC为直径的⊙O'上．

∵⊙O'的半径为1，

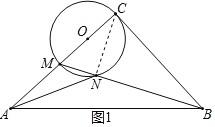
∴当点O'、N、A共线时，AN最小，如图2．在Rt△AO'C中，∵O'C=1，AC=2，∴O'A，

∴AN=AO'﹣O'N1，

即线段AN长度的最小值为1．

故答案为：1．