题目内容
【题目】阅读下面的情景对话，然后解答问题：
老师：我们新定义一种三角形，两边平方和等于第三边平方的2倍的三角形叫做奇异三角形．
小华：等边三角形一定是奇异三角形!
小明：那直角三角形是否存在奇异三角形呢？
（1）根据“奇异三角形”的定义，请你判断小华提出的命题：“等边三角形一定是奇异三角形”是真命题还是假命题？
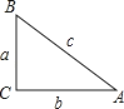
（2）在Rt△ABC中，AB＝c，AC＝b，BC＝a，且c＞b＞a，若Rt△ABC是奇异三角形，求a：b：c；
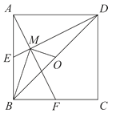
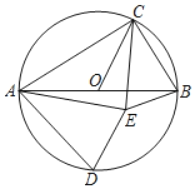
（3）如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆
中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．
①求证：△ACE是奇异三角形：
②当△ACE是直角三角形时，求∠AOC的度数．
【答案】（1）真命题，理由见解析；（2）
；（3）①见解析；②∠AOC的度数为60°或120°
【解析】
（1）根据“奇异三角形”的定义与等边三角形的性质，求证即可；
（2）根据勾股定理与奇异三角形的性质，可得a2+b2=c2与a2+c2=2b2，用a表示出b与c，即可求得答案；
（3）①AB是⊙O的直径，即可求得∠ACB=∠ADB=90°，然后利用勾股定理与圆的性质即可证得；
②利用（2）中的结论，分别从AC：AE：CE=1：
；与AC：AE：CE=
：
：1去分析，即可求得结果．
（1）设等边三角形的一边为a，则a2+a2＝2a2，
∴符合奇异三角形”的定义．
∴是真命题；
（2）∵∠C＝90°，
则a2+b2＝c2①，
∵Rt△ABC是奇异三角形，且b＞a，
∴a2+c2＝2b2②，
由①②得：b＝a，c＝a，
∴a：b：c＝1：；；
（3）∵①AB是⊙O的直径，
∴∠ACB＝∠ADB＝90°，
在Rt△ACB中，AC2+BC2＝AB2，
在Rt△ADB中，AD2+BD2＝AB2，
∵点D是半圆弧ADB的中点，
∴弧AD=弧BD，
∴AD＝BD，
∴AB2＝AD2+BD2＝2AD2，
∴AC2+CB2＝2AD2，
又∵CB＝CE，AE＝AD，
∴AC2+CE2＝2AE2，
∴△ACE是奇异三角形；
②由①可得△ACE是奇异三角形，
∴AC2+CE2＝2AE2，
当△ACE是直角三角形时，
由（2）得：AC：AE：CE＝1：或AC：AE：CE＝：：1，
当AC：AE：CE＝1：时，AC：CE＝1：，即AC：CB＝1：，
∵∠ACB＝90°，
∴∠ABC＝30°，
∴∠AOC＝2∠ABC＝60°；
当AC：AE：CE＝：：1时，AC：CE＝：1，即AC：CB＝：1，
∵∠ACB＝90°，
∴∠ABC＝60°，
∴∠AOC＝2∠ABC＝120°．
∴∠AOC的度数为60°或120°．
