��Ŀ����
����Ŀ��ϸ�ĵ�С�����֣�һԪ���η���ax2+bx+c��0��a��0������ϵ��֮��ġ����ܡ���ϵ��
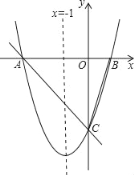
��1����x��1ʱ��a+b+c��0����x����1ʱ��a��b+c��0����9a+c��3b����x��
��2����2a+b��0��3a+c��0��д������������һ��һԪ���η��̣�������һ������
��3������ʦд������2x2��3x��1��0��Ҫ�ⷽ���жϸ������ʱ��С�������ش�����������ȵ�ʵ�������ݴˣ����ܸ���һԪ���η���ϵ��a��b��c�ķ����Լ��֮���������ϵ��д��һЩ����һԪ���η���ax2+bx+c��0��a��0������ϵ��֮��Ĺ�������дһд��������������
���𰸡���1��x����3��2��x2-3x-4=0;x2��4����3��������.
��������
��1��ֱ��ͨ���۲�Աȿɵó���.
��2���������֪һ����Ϊ-1���پ�������.
��3�����ݸ����б�ʽ��Τ�ﶨ�����.
��1����9a+c��3b��
��9a��3b+c��0��
��x����3��
��2����![]()
�ک��ٵã�a��b+c��0��
��x����1��
���������ķ��̿���Ϊ��x2��3x��4��0��
��x��4����x+1����0��
x1��4��x2����1��
��3��2x2��3x��1��0��
��Ϊa��2��c����1����֪��ac��0��
�����b2��4ac��0��
����һԪ���η���ϵ��a��b��c�ķ����Լ��֮���������ϵ���У��ٵ�a��c���ʱ������0����������������ȵ�ʵ����
���跽��ax2+bx+c��0������x1��x2������x1+x2��![]() ��x1x2��
��x1x2��![]() ��
��

 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�