题目内容
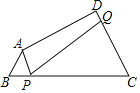
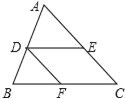
【题目】如图,在△ABC中,点D、E、F分别在边AB、AC、BC上,DE∥BC,DF∥AC,若△ADE与四边形DBCE的面积相等,则△DBF与△ADE的面积之比为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3-2
D. 3-2![]()
【答案】C
【解析】
根据矩形的性质得到DE=CF,根据相似三角形的性质得到![]() =(
=(![]() )2=
)2=![]() ,求得
,求得![]() =
=![]() ,设DE=
,设DE=![]() k,BC=2k,得到BF=2k-
k,BC=2k,得到BF=2k-![]() k,根据相似三角形的性质即可得到结论.
k,根据相似三角形的性质即可得到结论.
∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形,
∴DE=CF,
∵△ADE与四边形DBCE的面积相等,
∴![]() =
=![]() ,
,
∵DE∥BC,
∴△ADE∽△ABC,
∴![]() =(
=(![]() )2=
)2=![]() ,
,
∴![]() =
=![]() ,
,
设DE=![]() k,BC=2k,
k,BC=2k,
∴BF=2k-![]() k,
k,
∵DF∥AC,
∴△BDF∽△BAC,
∴△DBF∽△ADE,
∴![]() =(
=(![]() )2=
)2=![]() =
=![]() -1,
-1,
故选:C.

练习册系列答案
相关题目