题目内容
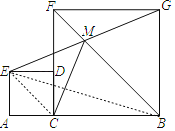
【题目】如图，线段AB＝4，点C为线段AB上任意一点（与端点不重合），分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBGF，分别连接BF、EG交于点M，连接CM，设AC＝x，S四边形ACME＝y，则y与x的函数表达式为y＝_____．
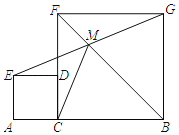
【答案】2x（0＜x＜4）
【解析】
连接CE，BE，如图，利用正方形的性质得到∠ACE＝∠CBF＝45°，则可判断CE∥BF，根据三角形面积公式得到S△CEB＝S△CEM，则y＝S△ABE＝
x4＝2x（0＜x＜4）．
连接CE，BE，如图，
∵四边形ACDE和四边形BCFG为正方形，
∴∠ACE＝∠CBF＝45°，
∴CE∥BF，
∴S△CEB＝S△CEM，
∴y＝S△ACE+S△CEM＝S△ACE+S△CEB＝S△ABE＝×AE×AB＝x4＝2x（0＜x＜4）．
故答案为y＝2x（0＜x＜4）．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
