题目内容
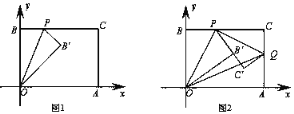
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)点C′不能落在边OA上.
;(4)点C′不能落在边OA上.
【解析】
(1)在Rt△OBP中,∠BOP=30°,求PB,即求P点坐标;
(2)证明OBP∽△PCQ,得到![]() 即可求解;
即可求解;
(3)OQ2=OA2+AQ2=42+AQ2=16+AQ2,当AQ最短时,OQ最短;
(4)假设点C′能落在边OA上,在Rt△OB′C′中,B′O2+B′C′2=OC′2,32+(4﹣2t)2=(4﹣t)2,△=(﹣8)2﹣4×3×9<0,该方程无实数解,点C′不能落在边OA上.
解:(1)∵A(4,0),B(0,3),
∴OA=4,OB=3,
在Rt△OBP中,
∵∠BOP=30°,
∴PB=![]() ,
,
∴点P的坐标为(![]() ,3),
,3),
(2)由题意,得BP=t,PC=4﹣t,CQ=3﹣m,
由折叠可知:∠OPB=∠OPB′,∠CPQ=∠C′PQ,
又∵∠OPB+∠OPB′+∠CPQ+∠C′PQ=180°,
∴∠OPB+∠CPQ=90°,
又∵∠OPB+∠BOP=90°,
∴∠OPB=∠CPQ,
又∵∠OBP=∠C=90°,
∴△OBP∽△PCQ,
∴![]() ,
,
![]() ,
,
∴m=![]() t2﹣
t2﹣![]() t+3;
t+3;
(3)∵OQ2=OA2+AQ2=42+AQ2=16+AQ2,
∴当AQ最短时,OQ最短,
∵AQ=m=![]() t2﹣
t2﹣![]() t+3=
t+3=![]() (t﹣2)2+
(t﹣2)2+![]() ,
,
∴当t=2时,AQ最短,OQ最短,
此时点Q(4,![]() ),
),
(4)点C′不能落在边OA上,
理由:假设点C′能落在边OA上,由折叠可得
PB=PB′=t,PC=PC′=4﹣t,OB=OB′=3,∠OPB=∠OPC′,∠OB′P=∠OBP=90°,
∵BC∥OA,
∴∠BPO=∠POC′,
∴∠OPC′=∠POC′,
∴OC′=PC′=4﹣t,
∴B′C′=PC﹣PB′=(4﹣t)﹣t=4﹣2t,
在Rt△OB′C′中,∵B′O2+B′C′2=OC′2,
∴32+(4﹣2t)2=(4﹣t)2,
整理,得3t2﹣8t+9=0,
∵△=(﹣8)2﹣4×3×9<0,
∴该方程无实数解,
∴点C′不能落在边OA上.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案