��Ŀ����
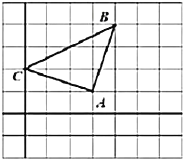
����Ŀ����ͼ1��ABCDΪ�����Σ��������εı�CB�Ƶ�C˳ʱ����ת��CE������BCE=��������BE��DE������C��CF��DE��F����ֱ��BE��H��
��1������=60��ʱ����ͼ1������BHC= ��
��2����45�㣼����90������ͼ2���߶�BH��EH��CH֮�����һ���ض���������ϵ������ͨ��̽����д�������ϵʽ�� ������֤������
��3����90�㣼����180���������������䣨��ͼ3������2���еĹ�ϵʽ�Ƿ�������������˵�����ɣ�����������д������Ϊ�����Ľ��ۣ�����Ҫ֤����

���𰸡���1��45�㣻��2��BH+EH=![]() CH����3����������BH��EH=
CH����3����������BH��EH=![]() CH��
CH��
�������������������1����CG��BH��G���������ε����ʺ���ת�����ʵó���BCE=��=60�㣬CB=CD=CE���ɵ��������ε����ʵó���BCG=��ECG=![]() ��BCE=30�㣬��ECF=��DCF=
��BCE=30�㣬��ECF=��DCF=![]() ��DCE�������GCH=
��DCE�������GCH=![]() ����BCE+��DCE��=45�㼴�ɣ�
����BCE+��DCE��=45�㼴�ɣ�
��2����CG��BH��G��ͬ��1���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ��ɵ���ֱ�������ε����ʺ��ɶ����ó�CH=![]() GH���ɵ��������ε����ʵó�BG=EG=
GH���ɵ��������ε����ʵó�BG=EG=![]() BE�����ɵó����ۣ�
BE�����ɵó����ۣ�
��3����CG��BH��G��ͬ��2���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ�CH=![]() GH��BG=EG=
GH��BG=EG=![]() BE�����ɵó����ۣ�
BE�����ɵó����ۣ�
����������⣺��1����CG��BH��G����ͼ1��ʾ��
���ı���ABCD�������Σ���CB=CD����BCD=90�㣬����ת�����ʵã�CE=CB����BCE=��=60�㣬��CD=CE����BCG=��ECG=![]() ��BCE=30�㣮��CF��DE�����ECF=��DCF=
��BCE=30�㣮��CF��DE�����ECF=��DCF=![]() ��DCE�����GCH=
��DCE�����GCH=![]() ����BCE+��DCE��=
����BCE+��DCE��=![]() ��90��=45�㣻�ʴ�Ϊ��45�㣻
��90��=45�㣻�ʴ�Ϊ��45�㣻
��2��BH+EH=![]() CH���������£�
CH���������£�
��CG��BH��G����ͼ2��ʾ��
ͬ��1���ã���BHC=45�㣬���CGH�ǵ���ֱ�������Σ���CH=![]() GH����CB=CE��CG��BE����BG=EG=
GH����CB=CE��CG��BE����BG=EG=![]() BE����BH+EH=BG+EG+EH+EH=2GH=
BE����BH+EH=BG+EG+EH+EH=2GH=![]() CH��
CH��
�ʴ�Ϊ��BH+EH=![]() CH��
CH��
��3����90�㣼����180�㣬�����������䣬��2���еĹ�ϵʽ��������BH��EH=![]() CH���������£�
CH���������£�
��CG��BH��G����ͼ3��ʾ��
ͬ��2���ã���BHC=45�㣬��CGH�ǵ���ֱ�������Σ�CH=![]() GH��BG=EG=
GH��BG=EG=![]() BE����BH��EH=BG+GH��EH=BG+EG��EH��EH=2GH=
BE����BH��EH=BG+GH��EH=BG+EG��EH��EH=2GH=![]() CH��
CH��