题目内容
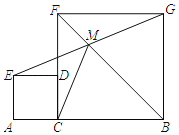
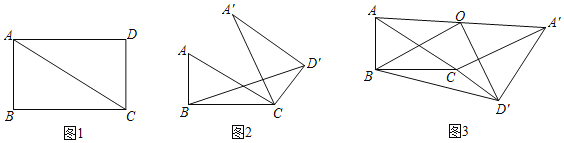
【题目】如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
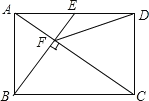
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
【答案】(1)3;(2)△OBD′是直角三角形;(3)90°或270°,240°或300°.
【解析】
(1)作D'E⊥BC于E,由直角三角形的性质得出BC=2![]() ,CE=
,CE=![]() CD'=1,D'E=
CD'=1,D'E=![]() ,由三角形面积公式即可得出答案;
,由三角形面积公式即可得出答案;
(2)连接OC,证明A、B、C、O四点共圆,由圆周角定理得出∠BOC=∠BAC=60°,同理A'、D'、C、O四点共圆,得出∠D'OC=∠D'A'C=30°,证出∠BOD'=90°即可;
(3)若B、C、D'三点不共线,证出BC=CD,这与已知相矛盾,得出B、C、D'三点共线;当α=α1时,OB=OD′,分两种情况:当点D'在BC的延长线上和当点D'在边BC上;当α=α2时,△OBD′不存在时,分两种情况:当O与D'重合时,当O与B重合时,由等腰三角形的性质和等边三角形的性质即可得出答案.
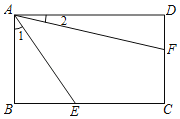
解:(1)作D'E⊥BC交BC的延长线于E,如图2所示:
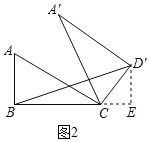
则∠E=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AB∥CD,AD∥BC,CD=AB=2,
∴∠ACD=∠BAC,∠DAC=∠ACB=30°,
∵∠ACB=30°,
∴BC=![]() AB=2
AB=2![]() ,∠ACD=∠BAC=60°,
,∠ACD=∠BAC=60°,
由旋转的性质得:CD'=CD=2,∠ACA'=30°,
∴∠D'CE![]() ,
,
∴∠CD'E![]() ,
,
∴CE=![]() CD'=1,D'E=
CD'=1,D'E=![]() CE=
CE=![]() ,
,
∴S△BCD′=![]() BC×D'E=
BC×D'E=![]() ×2
×2![]() ×
×![]() =3;
=3;
(2)△OBD′是直角三角形,理由如下:
连接OC,如图3所示:
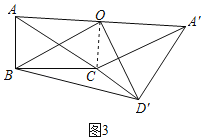
由旋转的性质得:CA'=CA,∠A'D'C=∠ADC=90°,∠D'A'C=∠DAC=30°,
∵O是AA′的中点,
∴OC⊥AA',
∴∠AOC=∠A'OC=![]() =∠ABC=∠A'D'C,
=∠ABC=∠A'D'C,
∴∠ABC+∠AOC=180°,
∴A、B、C、O四点共圆,
∴∠BOC=∠BAC=60°,
同理;A'、D'、C、O四点共圆,
∴∠D'OC=∠D'A'C=30°,
∴∠BOD'=90°,
∴△BOD'是直角三角形;
(3)若B、C、D'三点不共线,如图3所示:
由(2)得:∠OBC=∠OAC,∠OD'C=∠OA'C,∠OAC=∠OA'C,
∴∠OBC=∠OD'C,
∵OB=O D',
∴∠OBD'=∠OD'B,
∴∠CBD'=∠CD'B,
∴CB=CD',
∵CD'=CD,
∴BC=CD,这与已知相矛盾,
∴B、C、D'三点共线;
分两种情况:当点D'在BC的延长线上时,如图4所示:
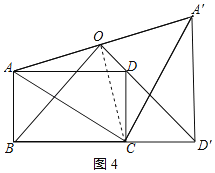
∵∠ACB=![]() ,∠A'CD'=∠ACD=
,∠A'CD'=∠ACD=![]() ,
,
∴∠AC A'![]() ,
,
∴α=α1![]() ;
;
当点D'在边BC上时,如图5所示:
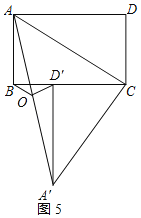
∵∠ACB=![]() ,∠A'CD'=∠ACD=
,∠A'CD'=∠ACD=![]() ,
,
∴∠AC A'=![]() ,
,
∴α=α1![]() ;
;
故答案为:90°或270;
当α=α2时,△OBD′不存在时,分两种情况:
当O与D'重合时,如图6所示:
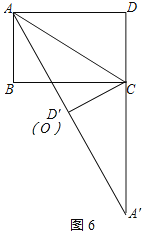
∵CA'=CA,∠CAD'=∠CA'D'=![]() ,
,
∴∠ACA'=120°,
∴α=α2![]() ;
;
当O与B重合时,如图7所示:
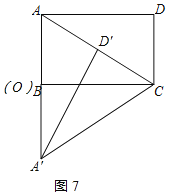
则AA'=2AB=4,
∵CA=CA'=2AB=4=AA',
∴△ACA'是等边三角形,
∴∠A'CA=60°,
∴α=α2![]() ;
;
故答案为:240°或300.

 互动英语系列答案
互动英语系列答案【题目】甲、乙两人进行射击比赛,两人4次射击的成绩(单位:环)如下:
甲:8,6,9,9;
乙:7,8,9,8.
(1)请将下表补充完整:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 1.5 | ||
乙 | 8 | 8 |
(2)谁的成绩较稳定?为什么?
(3)分别从甲、乙两人的成绩中随机各选取一次,则选取的两个成绩之和为16环的概率是多少?