题目内容
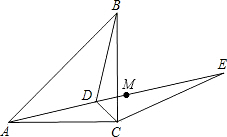
如图,△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,BM交CD于点E,且点E为CD的中点,连接MD,过点D作ND⊥MD于点D,DN交BM于点N.
(1)若BC= ,求△BDE的周长;
,求△BDE的周长;
(2)求证:NE-ME=CM.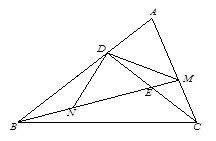
(1)若BC=
 ,求△BDE的周长;
,求△BDE的周长;(2)求证:NE-ME=CM.
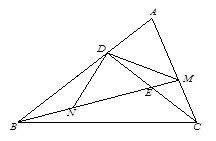
(1)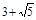 ;(2)完成证明见解析
;(2)完成证明见解析
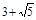 ;(2)完成证明见解析
;(2)完成证明见解析试题分析:(1)充分利用直角三角形的性质和勾股定理即可得解,在Rt△BDE中,要求周长,求出是BD长是关键,而BD长放在Rt△BCD中即可得解.
(2)想证明NE-ME=CM这样的关系,关键将其放入全等三角形中,用等量代换的关系即可得证,充分利用点E为CD的中点的条件作出辅助线,过D作D作DF⊥BM于点F,或过点D作DF∥CM交BM于点F,或在MB上截取EF,使EF=EM(如第24题解答图1),另外也可过点C作CP∥DN交BM延长线于点P,或过点C作CP∥DN交BM延长线于点P,或延长EM至点P,使EP=EN(如第24题解答图2),利用两次全等三角形,即可得证。
试题解析:
(1)∵∠ABC=45°,CD⊥AB
∴在Rt△BCD中,∠DBC=∠DCB="45°"
∵BC=
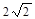 ∴BD="CD=2"
∴BD="CD=2" ∵点E为CD中点
∴DE=CE=
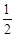 CD="1"
CD="1" ∴
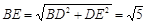
∴
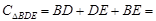
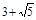
∴△BDE的周长为
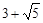
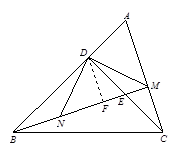
(2)(方法一)过点D作DF⊥BM于点F
∵BM⊥AC
∴∠DFE=∠CME=90°
在△DEF和△CEM中
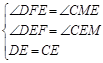
∴△DEF≌△CEM(AAS)
∴DF=CM FE=ME
∵ND⊥MD,CD⊥AB
∴∠BDN+∠NDE=∠CDM+∠NDE=90°
∴∠BDN=∠CDM
∵CD⊥AB,BM⊥AC
∴∠BDE=∠CDA="90°"
∠DBE+∠DEB=∠ACD+∠CEM=90°
∵∠DEB=∠CEM ∴∠DBE=∠ACD
在△BDN和△CDM中
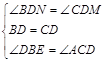
∴△BDN≌△CDM(ASA)
∴DN=DM
∴在Rt△DMN中,∠DNM=∠DMN=45°
∴在Rt△DMN中,∠DNM=∠NDF=45°
∴DF="NF"
又∵DF=CM,FE=ME
∴NE=NF+FE=CM+ME
∴NE-ME="CM."
(2)问其他方法:(解法略)

方法二:过点D作DF∥CM交BM于点F
方法三:在MB上截取EF,使EF=EM
方法四:过点C作CP∥DN交BM延长线于点P
方法五:延长EM至点P,使EP=EN

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
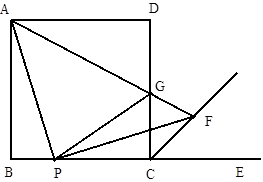
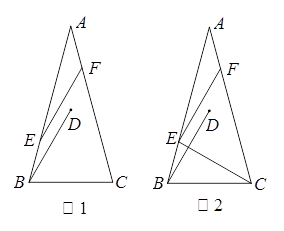
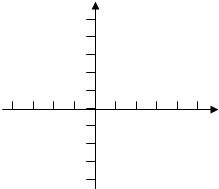

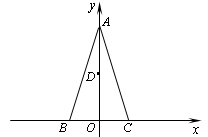
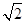 ),C(1,0), D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为( )
),C(1,0), D为射线AO上一点,一动点P从A出发,运动路径为A→D→C,点P在AD上的运动速度是在CD上的3倍,要使整个运动时间最少,则点D的坐标应为( )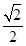 )
) )
)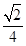 )
)