题目内容
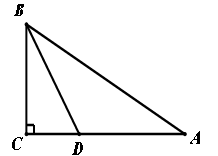
如图,△ABC中,∠C=90°,∠A=30°,BD平分∠CBA交AC于点D,若CD=2cm,则AD= cm。

6.
试题分析:根据∠C=90°,∠A=30°,易求∠ABC=60°,而BD是角平分线,易得∠ABD=∠DBC=30°,那么易证△ABD是等腰三角形,且△BCD是含有30°角的直角三角形,易求BD,从而可求CD.
试题解析:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
又∵BD是角平分线,
∴∠ABD=∠DBC=30°,
在Rt△BCD中,BD=2CD=4cm,
又∵∠A=∠ABD=30°,
∴AD=BD=4cm,
∴AC=6cm.
考点: 1.角平分线的性质;2.含30度角的直角三角形.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
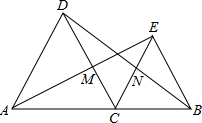
 ,求△BDE的周长;
,求△BDE的周长;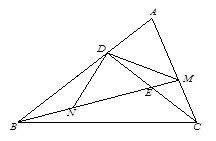
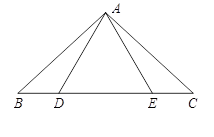
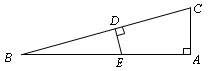
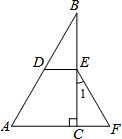
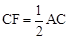 ,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________
,DE是△ABC中位线,如果∠1=30°,DE=2,则四边形AFED的周长是________