题目内容
已知A（2，0），B（0，2），试在x轴上确定点M，使三角形MAB是等腰三角形，写出所有满足条件点M的坐标．
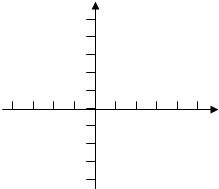
（0，0）（?2，0）（2+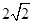
，0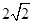），（?+2，0）．
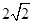，0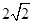），（?+2，0）．如图所示：M1（0，0），M4（?2，0），
∵A（2，0），B（0，2），∴AB=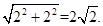
，
∵M2，M3是以A为圆心，AB长为半径交x轴于两点，
∴M2（2+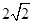，0），M3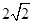（?+2，0）．
故所有满足条件点M的坐标是：（0，0）（?2，0）（2+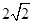，0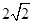），（?+2，0）．
∵A（2，0），B（0，2），∴AB=
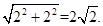，∵M2，M3是以A为圆心，AB长为半径交x轴于两点，
∴M2（2+
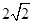，0），M3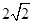（?+2，0）．故所有满足条件点M的坐标是：（0，0）（?2，0）（2+
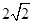，0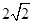），（?+2，0）．
练习册系列答案
相关题目
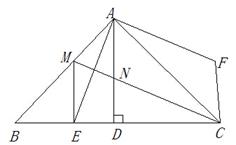
AC长为半径画弧，两弧相交于点M、N，作直线MN，与AC交于点D，与BC交于点E，连接AE.
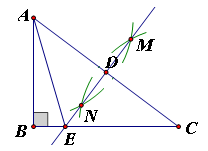
，求△BDE的周长；
