ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥Ή‘––≥ΒΨ≠”ΣΒξœζ έ![]() –ΆΘ§
–ΆΘ§![]() –ΆΝΫ÷÷ΤΖ≈ΤΉ‘––≥ΒΘ§ΫώΡξΫχΜθΚΆœζ έΦέΗώ»γœ¬±μΘΚ(ΫώΡξ1ΡξΡΎΉ‘––≥ΒΒΡ έΦέ”κΫχΦέ±Θ≥÷≤Μ±δ)
–ΆΝΫ÷÷ΤΖ≈ΤΉ‘––≥ΒΘ§ΫώΡξΫχΜθΚΆœζ έΦέΗώ»γœ¬±μΘΚ(ΫώΡξ1ΡξΡΎΉ‘––≥ΒΒΡ έΦέ”κΫχΦέ±Θ≥÷≤Μ±δ)
|
| |
ΫχΜθΦέΗώ(‘Σ/ΝΨ) | 1000 | 1100 |
œζ έΦέΗώ(‘Σ/ΝΨ) |
| 1500 |
ΫώΡξΨ≠ΙΐΗΡ‘λ…ΐΦΕΚσΘ§![]() –Ά≥ΒΟΩΝΨœζ έΦέ±»»ΞΡξ‘ωΦ”400‘ΣΘ°“―÷Σ
–Ά≥ΒΟΩΝΨœζ έΦέ±»»ΞΡξ‘ωΦ”400‘ΣΘ°“―÷Σ![]() –Ά≥Β»ΞΡξ1‘¬Ζίœζ έΉήΕνΈΣ3.6Άρ‘ΣΘ§ΫώΡξ1‘¬Ζί
–Ά≥Β»ΞΡξ1‘¬Ζίœζ έΉήΕνΈΣ3.6Άρ‘ΣΘ§ΫώΡξ1‘¬Ζί![]() –Ά≥ΒΒΡœζ έ ΐΝΩ”κ»ΞΡξ1‘¬ΖίœύΆ§Θ§Εχœζ έΉήΕν±»»ΞΡξ1‘¬Ζί‘ωΦ”
–Ά≥ΒΒΡœζ έ ΐΝΩ”κ»ΞΡξ1‘¬ΖίœύΆ§Θ§Εχœζ έΉήΕν±»»ΞΡξ1‘¬Ζί‘ωΦ”![]() Θ°
Θ°
Θ®1Θ©»τ…ηΫώΡξ1‘¬ΖίΒΡ![]() –ΆΉ‘––≥Β έΦέΈΣ
–ΆΉ‘––≥Β έΦέΈΣ![]() ‘Σ/ΝΨΘ§«σ
‘Σ/ΝΨΘ§«σ![]() ΒΡ÷ΒΘΩ(”ΟΝ–ΖΫ≥ΧΒΡΖΫΖ®Ϋβ¥π)
ΒΡ÷ΒΘΩ(”ΟΝ–ΖΫ≥ΧΒΡΖΫΖ®Ϋβ¥π)
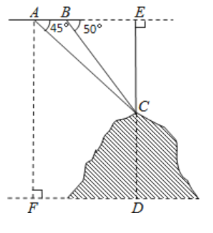
Θ®2Θ©ΗΟΒξΦΤΜ°8‘¬Ζί‘ΌΫχ“Μ≈ζ![]() –ΆΚΆ
–ΆΚΆ![]() –ΆΉ‘––≥ΒΙ≤50ΝΨΘ§«“
–ΆΉ‘––≥ΒΙ≤50ΝΨΘ§«“![]() –Ά≥Β ΐΝΩ≤Μ≥§Ιΐ
–Ά≥Β ΐΝΩ≤Μ≥§Ιΐ![]() –Ά≥Β ΐΝΩΒΡ2±ΕΘ§”Π»γΚΈΫχΜθ≤≈Ρή Ι’β≈ζΉ‘––≥ΒΜώάϊΉνΕύΘΩ
–Ά≥Β ΐΝΩΒΡ2±ΕΘ§”Π»γΚΈΫχΜθ≤≈Ρή Ι’β≈ζΉ‘––≥ΒΜώάϊΉνΕύΘΩ
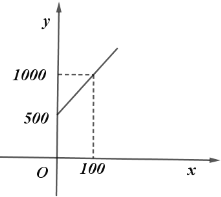
Θ®3Θ©ΗΟΒξΈΣΈϋ“ΐΩΆ‘¥Θ§ΉΦ±Η‘ωΙΚ“Μ÷÷ΫχΦέΈΣ500‘ΣΒΡ![]() –Ά≥ΒΘ§‘ΛΥψ”Ο8Άρ‘ΣΙΚΫχ’β»ΐ÷÷≥Β»τΗ…ΝΨΘ§Τδ÷–
–Ά≥ΒΘ§‘ΛΥψ”Ο8Άρ‘ΣΙΚΫχ’β»ΐ÷÷≥Β»τΗ…ΝΨΘ§Τδ÷–![]() –Ά”κ
–Ά”κ![]() –ΆΒΡ ΐΝΩ÷°±»ΈΣ
–ΆΒΡ ΐΝΩ÷°±»ΈΣ![]() Θ§‘ρΗΟΒξ÷Ν…ΌΩ…“‘ΙΚΫχ»ΐ÷÷≥ΒΙ≤Εύ…ΌΝΨΘΩ
Θ§‘ρΗΟΒξ÷Ν…ΌΩ…“‘ΙΚΫχ»ΐ÷÷≥ΒΙ≤Εύ…ΌΝΨΘΩ
ΓΨ¥πΑΗΓΩΘ®1Θ©ΫώΡξ1‘¬ΖίΒΡ![]() –ΆΉ‘––≥Β έΦέΈΣ1200‘ΣΘΜΘ®2Θ©
–ΆΉ‘––≥Β έΦέΈΣ1200‘ΣΘΜΘ®2Θ©![]() –ΆΫχ17ΝΨΘ§
–ΆΫχ17ΝΨΘ§![]() –ΆΫχ33ΝΨ ±ΜώάϊΉνΕύΘΜΘ®3Θ©ΗΟΒξ÷Ν…ΌΩ…“‘Ι≤ΙΚΫχ92ΝΨΘ°
–ΆΫχ33ΝΨ ±ΜώάϊΉνΕύΘΜΘ®3Θ©ΗΟΒξ÷Ν…ΌΩ…“‘Ι≤ΙΚΫχ92ΝΨΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©…ηΫώΡξ1‘¬ΖίΒΡ![]() –ΆΉ‘––≥Β έΦέΈΣ
–ΆΉ‘––≥Β έΦέΈΣ![]() ‘ΣΘ§ΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§«σΫβΦ¥Ω…ΘΜ
‘ΣΘ§ΗυΨίΧβ“βΝ–≥ωΖΫ≥ΧΘ§«σΫβΦ¥Ω…ΘΜ
Θ®2Θ©…ηΙΚ¬ρ![]() –ΆΉ‘––≥Β
–ΆΉ‘––≥Β![]() ΝΨΘ§ΗυΨί
ΝΨΘ§ΗυΨί![]() –Ά≥Β ΐΝΩ≤Μ≥§Ιΐ
–Ά≥Β ΐΝΩ≤Μ≥§Ιΐ![]() –Ά≥Β ΐΝΩΒΡ2±ΕΝ–≥ω≤ΜΒ» Ϋ«σ≥ωaΒΡΖΕΈßΘ§‘ΌΝ–≥ωWΚΆaΒΡΙΊœΒ ΫΘ§Ψί¥Υ«σ≥ωWΒΡΉν¥σ÷ΒΦ¥Ω…ΘΜ
–Ά≥Β ΐΝΩΒΡ2±ΕΝ–≥ω≤ΜΒ» Ϋ«σ≥ωaΒΡΖΕΈßΘ§‘ΌΝ–≥ωWΚΆaΒΡΙΊœΒ ΫΘ§Ψί¥Υ«σ≥ωWΒΡΉν¥σ÷ΒΦ¥Ω…ΘΜ
Θ®3Θ©…ηΙΚΫχ![]() –Ά
–Ά![]() ΝΨΘ§‘ρ
ΝΨΘ§‘ρ![]() –Ά
–Ά![]() ΝΨΘ§
ΝΨΘ§![]() –Ά
–Ά![]() ΝΨΘ§Ν–≥ωnΚΆaΒΡΖΫ≥ΧΘ§Ϋβ≥ω
ΝΨΘ§Ν–≥ωnΚΆaΒΡΖΫ≥ΧΘ§Ϋβ≥ω![]() Θ§ΒΟΒΫΒ±
Θ§ΒΟΒΫΒ±![]() ±Θ§
±Θ§![]() Ήν–Γ÷ΒΈΣ92.
Ήν–Γ÷ΒΈΣ92.
ΫβΘΚΘ®1Θ©…ηΫώΡξ1‘¬ΖίΒΡ![]() –ΆΉ‘––≥Β έΦέΈΣ
–ΆΉ‘––≥Β έΦέΈΣ![]() ‘ΣΘ§
‘ΣΘ§
‘ρ»ΞΡξ![]() ––Ή‘––≥Β έΦέΈΣ
––Ή‘––≥Β έΦέΈΣ![]() ‘ΣΘ°
‘ΣΘ°
ΗυΨίΧβ“βΘ§ΒΟ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§
Ψ≠Φλ―ιΘ§![]() «ΥυΝ–Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
«ΥυΝ–Ζ÷ ΫΖΫ≥ΧΒΡΫβΘ§
ΓύΫώΡξ1‘¬ΖίΒΡ![]() –ΆΉ‘––≥Β έΦέΈΣ1200‘ΣΘΜ
–ΆΉ‘––≥Β έΦέΈΣ1200‘ΣΘΜ
Θ®2Θ©…ηΙΚ¬ρ![]() –ΆΉ‘––≥Β
–ΆΉ‘––≥Β![]() ΝΨΘ§‘ρ
ΝΨΘ§‘ρ![]() –ΆΉ‘––≥Β
–ΆΉ‘––≥Β![]() ΝΨΘ§
ΝΨΘ§
![]()
ΫβΒΟΘΚ![]() Θ§«“
Θ§«“![]() ΈΣ’ϊ ΐ
ΈΣ’ϊ ΐ
Υυ“‘άϊ»σ![]()
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΒΡ‘ω¥σΕχΦθ–ΓΘ§
ΓύΒ±![]() ±Θ§Φ¥
±Θ§Φ¥![]() –ΆΫχ17ΝΨΘ§
–ΆΫχ17ΝΨΘ§![]() –ΆΫχ33ΝΨ ±ΜώάϊΉνΕύΘ°
–ΆΫχ33ΝΨ ±ΜώάϊΉνΕύΘ°
Θ®3Θ©…ηΙΚΫχ![]() –Ά
–Ά![]() ΝΨΘ§‘ρ
ΝΨΘ§‘ρ![]() –Ά
–Ά![]() ΝΨΘ§
ΝΨΘ§![]() –Ά
–Ά![]() ΝΨΘ§
ΝΨΘ§
ΗυΨίΧβ“βΘ§ΒΟΘΚ![]()
ΫβΒΟΘΚ![]() Θ§
Θ§
“ρΈΣ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§«“
Θ§«“![]() ΈΣ’ϊ ΐΘ§
ΈΣ’ϊ ΐΘ§
“ρΈΣ![]() ΈΣ’ϊ ΐΘ§Υυ“‘
ΈΣ’ϊ ΐΘ§Υυ“‘![]() ΈΣ5ΒΡ±Ε ΐΘ§
ΈΣ5ΒΡ±Ε ΐΘ§
ΓύΒ±![]() ±Θ§
±Θ§![]() Ήν–Γ÷ΒΈΣ92Θ§
Ήν–Γ÷ΒΈΣ92Θ§
¥πΘΚΗΟΒξ÷Ν…ΌΩ…“‘Ι≤ΙΚΫχ92ΝΨ.

 ”≈―ßΟϊ ΠΟϊΧβœΒΝ–¥πΑΗ
”≈―ßΟϊ ΠΟϊΧβœΒΝ–¥πΑΗ