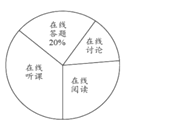
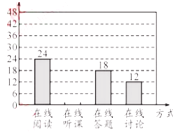
题目内容
【题目】如图,在![]() 中,
中,![]() 点
点![]() 为直线
为直线![]() 上一点,点
上一点,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,连接
,连接![]() .
.
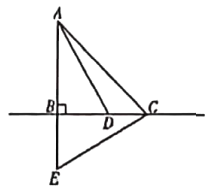
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 的度数;
的度数;
![]() 点
点![]() 是
是![]() 的外心,当点
的外心,当点![]() 在直线
在直线![]() 上运动,且点
上运动,且点![]() 恰好在
恰好在![]() 内部或边上时,直接写出点
内部或边上时,直接写出点![]() 运动的路径的长,
运动的路径的长,
【答案】(1)见解析;(2):∠E=65°或25°;(3)![]()
【解析】
(1)(1)利用“边角边”证明即可;
(2)分两种情况:点D在线段BC上时和点D在BC延长线上时,利用全等三角形对应角相等,推出∠E=∠ADB,再根据等腰直角三角形的性质求出∠ACB=∠CAB=45°,根据外角性质求出∠ADB,即可解答;
(3)过点B作BF垂直AC,交AC于F,作DC边的垂直平分线交BF于点P,过点F作FG⊥BC,交BC于点G,证明BF是AC的垂直平分线,从而推出点P即为三角形CAD的外心,根据点![]() 恰好在
恰好在![]() 内部或边上,确定点
内部或边上,确定点![]() 运动的路径为BF,求BF的长即可.
运动的路径为BF,求BF的长即可.
(1)∵∠ABC=90°,
∴∠CBE=90°=∠ABC,
∵AB=CB, BE=BD,
∴ △ABD≌△CBE;
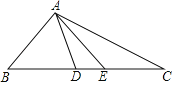
(2)当点D在线段BC上时,
∵△ABD≌△CBE,
∴∠E=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠E=∠ADB=45°+20°=65°;
当点D在BC延长线上时,如图,
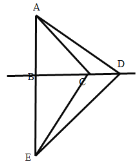
∵△ABD≌△CBE,
∴∠BEC=∠ADB,
∵AB=CB,∠ABC=90°,
∴∠ACB=∠BAC=45°,
∴∠BEC=∠ADB=45°-20°=25°;
综上:∠E=65°或25°.
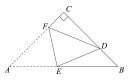
(3)如图,过点B作BF垂直AC,交AC于F,作DC边的垂直平分线交BF于点P,过点F作FG⊥BC,交BC于点G,
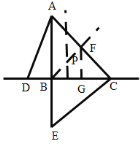
∵![]() BF⊥AC,
BF⊥AC,
∴BF是AC的垂直平分线,
∴点P即为三角形CAD的外心.
∵P为BF上一点,
由题意可知点![]() 恰好在
恰好在![]() 内部或边上,
内部或边上,
∴点![]() 运动的路径为BF,
运动的路径为BF,
∵![]()
∴![]() ,
,
∵BF是AC的垂直平分线,
∴BF=![]() ,
,
即点P的运动路径长为![]()

【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?