题目内容
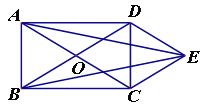
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.
【答案】(1)证明见解析;(2)AE=BE,理由见解析.
【解析】
试题(1)先判断四边形OCDE是平行四边形,又因为四边形ABCD是矩形,两个结论联合起来,可知四边形OCDE是菱形;
(2)先证出∠ADE=∠BCE,再证明△ADE≌△BCE,从而得出AE=BE.
试题解析:(1)四边形OCDE是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCDE是平行四边形,
∵矩形ABCD的对角线AC、BD相交于点O,
∴OC=![]() AC=
AC=![]() BD=OD,
BD=OD,
∴四边形OCDE是菱形;
(2)AE=BE,理由是:
∵四边形ABCD是矩形,
∴AD=BC,∠ADC=∠BCD,
∵四边形OCDE是菱形,
∴ED=EC,∠EDC=∠ECD,
∴∠EDC+∠ADC =∠ECD+∠BCD,
即:∠ADE =∠BCE
在△ADE和△BCE中,
∵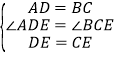 ,
,
∴△ADE≌△BCE,
∴AE=BE.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目