题目内容
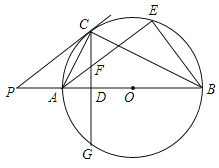
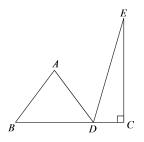
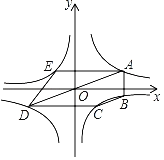
【题目】如图,经过原点O的直线与反比例函数y=![]() (a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=
(a>0)的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数y=![]() (b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,
(b<0)的图象上,AB∥y轴,AE∥CD∥x轴,五边形ABCDE的面积为56,四边形ABCD的面积为32,则a﹣b的值为__,![]() 的值为__.
的值为__.
【答案】24 ﹣![]()
【解析】
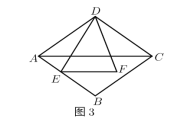
如图,连接AC,OE,OC,OB,延长AB交DC的延长线于T,设AB交x轴于K.求出证明四边形ACDE是平行四边形,推出S△ADE=S△ADC=S五边形ABCDE-S四边形ABCD=56-32=24,推出S△AOE=S△DEO=12,可得![]() a-
a-![]() b=12,推出a-b=24.再证明BC∥AD,证明AD=3BC,推出AT=3BT,再证明AK=3BK即可解决问题.
b=12,推出a-b=24.再证明BC∥AD,证明AD=3BC,推出AT=3BT,再证明AK=3BK即可解决问题.
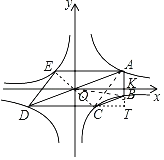
如图,连接AC,OE,OC,OB,延长AB交DC的延长线于T,设AB交x轴于K.
由题意A,D关于原点对称,
∴A,D的纵坐标的绝对值相等,
∵AE∥CD,
∴E,C的纵坐标的绝对值相等,
∵E,C在反比例函数y=![]() 的图象上,
的图象上,
∴E,C关于原点对称,
∴E,O,C共线,
∵OE=OC,OA=OD,∴四边形ACDE是平行四边形,
∴S△ADE=S△ADC=S五边形ABCDE﹣S四边形ABCD=56﹣32=24,
∴S△AOE=S△DEO=12,
∴![]() a﹣
a﹣![]() b=12,
b=12,
∴a﹣b=24,
∵S△AOC=S△AOB=12,
∴BC∥AD,
∴![]() =
=![]() ,
,
∵S△ACB=32﹣24=8,
∴S△ADC:S△ABC=24:8=1:3,
∴BC:AD=1:3,
∴TB:TA=1:3,设BT=a,则AT=3a,AK=TK=1.5k,BK=0.5k,
∴AK:BK=3:1,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =﹣
=﹣![]() .
.
故答案为24,﹣![]() .
.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?