题目内容
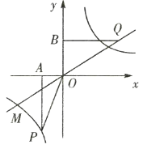
【题目】如图,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,与反比例函数
两点,与反比例函数![]()
![]() 的图像交于点
的图像交于点![]() ,且
,且![]() .
.
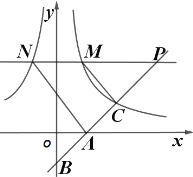
(1)求反比例函数的解析式;
(2)点![]()
![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的平行线交反比例函数
轴的平行线交反比例函数![]()
![]() 和
和![]()
![]() 的图像于
的图像于![]() ,
,![]() 两点,连
两点,连![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由直线l:y=x﹣1与x轴、y轴交于A、B两点,即可求得点A与B的坐标,又由与反比例函数![]() 的图象交于点C,且AB=AC,可求得点C的坐标,再利用待定系数法求得反比例函数的解析式;
的图象交于点C,且AB=AC,可求得点C的坐标,再利用待定系数法求得反比例函数的解析式;
(2)由点P(n+1,n)(n>1)是直线l上一点,过点P作x轴的平行线交反比例函数![]() 和
和![]() 的图象于M,N两点,可表示出M,N两点的坐标,继而表示出PM,PN,PC,PA的长,由MC∥NA,可得
的图象于M,N两点,可表示出M,N两点的坐标,继而表示出PM,PN,PC,PA的长,由MC∥NA,可得![]() =
=![]() ,继而可得方程:
,继而可得方程: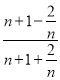 =
=![]() ,解此方程即可求得答案.
,解此方程即可求得答案.
(1)∵y=x﹣1与x轴、y轴交于A、B两点,
∴点A的坐标为:(1,0),点B的坐标为:(0,﹣1),
∴![]() ,
,
∵AB=AC,A,B,C都在直线l上,
过点C作CD⊥x轴于点D,如图,
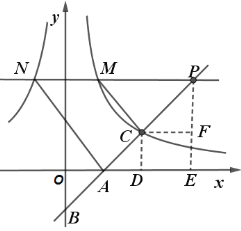
又∵∠OAB=∠DAC,∠BOA=∠CDA=90°
∴![]() ,
,
∴![]() ,
,
∴点C的坐标为(2,1),
∵点C在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴1=![]() ,
,
解得:k=2,
∴反比例函数的解析式为:y=![]() ;
;
(2)∵点P(n+1,n)(n>1)是直线l上一点,过点P作x轴的平行线交反比例函数y=![]() 与y=﹣
与y=﹣![]() 的图象于M,N两点,
的图象于M,N两点,
∴M(![]() ,n),N(﹣
,n),N(﹣![]() ,2),
,2),
∴PM=n+1﹣![]() ,PN=n+1+
,PN=n+1+![]() ,
,![]() ,
,![]() ,
,
∵MC∥NA,
∴![]() =
=![]() ,
,
即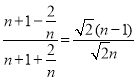 ,
,
整理得:n2﹣3n+2=0,
解得:n1=2,n2=1(舍去),
∴n=2.

 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?