题目内容
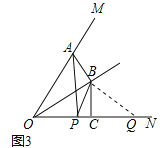
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发行了两枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理,如图的勾股图中,已知![]() ,
,![]() ,
,![]() .作四边形
.作四边形![]() ,满足点
,满足点![]() 、
、![]() 在边
在边![]() 上,点
上,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,
,![]() 、
、![]() 是直线
是直线![]() 与
与![]() ,
,![]() 的交点.那么
的交点.那么![]() 的长等于( )
的长等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
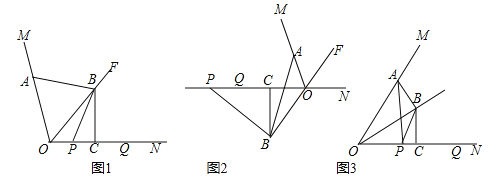
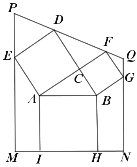
先根据勾股定理求出BC的长,双向延长线段AB交PM于点O,交QN于点R,则AO⊥MP,BR⊥QN,如图1,然后根据平角的定义、直角三角形的性质和等量代换可得∠4=∠5,根据SAS易证△ABC≌△DFC,可得DF=AB=5,∠6=∠1,∠8=∠5,进而可得∠7=∠4,于是有PD=PE,作PS⊥DE于点S,如图2,则在Rt△PDS中,利用三角函数的知识可求出PD的长,作QW⊥FG于点W,同理可求出FQ的长,进一步即可求出结果.
解:在△ABC中,∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
双向延长线段AB交PM于点O,交QN于点R,则AO⊥MP,BR⊥QN,如图1,
由题意得:∠1+∠2=90°,∠3+∠2=90°,∠3+∠4=90°,∠1+∠5=90°,
∴∠4=∠5,
∵AC=DC,∠ACB=∠DCF=90°,CF=CB,
∴△ABC≌△DFC(SAS),
∴DF=AB=5,∠6=∠1,∠8=∠5,
∵∠6+∠7=90°,∠6+∠8=90°,
∴∠7=∠8,
∴∠7=∠4,
∴PD=PE,
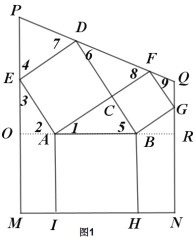
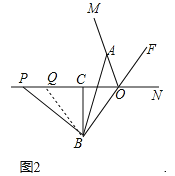
作PS⊥DE于点S,如图2,则![]() ,
,
在Rt△PDS中,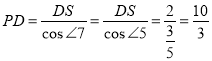 ;
;
同理可得:QF=QG,∠9=∠1,
作QW⊥FG于点W,则![]() ,
,
在Rt△FQW中,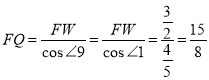 ;
;
∴![]() .
.
故选:A.

【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?