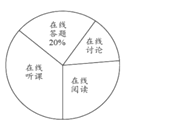
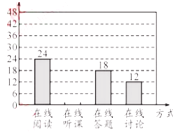
��Ŀ����
����Ŀ��Ϊ���Ż�����������ijһС�����������̻������мס��������̻���˾������Ͷ�꣬�����Ƴ����̻��շѷ������£���˾�̻�����![]() ��Ԫ�� ���̻����
��Ԫ�� ���̻����![]() ��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ��
��ƽ���ף���һ�κ�����ϵ����ͼ��ʾ��
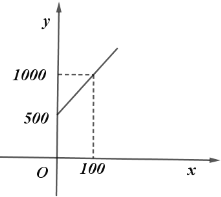
�ҹ�˾���̻����������1000ƽ����ʱ��ͳһ��ȡ����5000Ԫ���̻��������1000ƽ����ʱ����������ÿƽ������ȡ3Ԫ��
��1����ס��ҹ�˾�̻�����![]() ��Ԫ�����̻����
��Ԫ�����̻����![]() ��ƽ���ף��ĺ�������ʽ��
��ƽ���ף��ĺ�������ʽ��
��2�������С��Ŀǰ���̻������1500ƽ���ף���ͨ������˵����ѡ���ļҹ�˾���̻����ý��٣�
���𰸡���1����˾y����x�ĺ�������ʽΪy��=5x+500���ҹ�˾����x�ĺ�������ʽΪy=![]() ����2��ѡ���ҹ�˾�̻����ý��٣�
����2��ѡ���ҹ�˾�̻����ý��٣�
��������
��1������ϵ�������������˾����ʽ���ֶκ�����ʾ�ҹ�˾��������ʽ��
��2����x=1500����������ʽ���ɽ��.
�⣺��1�����˾y����x�ĺ�������ʽΪy=kx+b��k��0����
����ͼ����0��500������100��1000��
��![]()
��k=5��b=500��
���˾y����x�ĺ�������ʽΪy��=5x+500��
y��=5000��0��x��1000����
y��=3(x��1000)+5000����y��=3x+2000��x��1000����
���ҹ�˾y����x�ĺ�������ʽΪy=![]() ��
��
��2����x=1500ʱ��y��=5x+500=8000��Ԫ����
��x=1500ʱ��y��=3x+2000=6500��Ԫ����
��8000��6500��
��ѡ���ҹ�˾�̻����ý��٣�

����Ŀ��ij���г���Ӫ������![]() �ͣ�
�ͣ�![]() ������Ʒ�����г���������������ۼ۸����±���(����1�������г����ۼ�����۱��ֲ���)
������Ʒ�����г���������������ۼ۸����±���(����1�������г����ۼ�����۱��ֲ���)
|
| |
�����۸�(Ԫ/��) | 1000 | 1100 |
���ۼ۸�(Ԫ/��) |
| 1500 |
���꾭������������![]() �ͳ�ÿ�����ۼ۱�ȥ������400Ԫ����֪
�ͳ�ÿ�����ۼ۱�ȥ������400Ԫ����֪![]() �ͳ�ȥ��1�·������ܶ�Ϊ3.6��Ԫ������1�·�
�ͳ�ȥ��1�·������ܶ�Ϊ3.6��Ԫ������1�·�![]() �ͳ�������������ȥ��1�·���ͬ���������ܶ��ȥ��1�·�����
�ͳ�������������ȥ��1�·���ͬ���������ܶ��ȥ��1�·�����![]() ��
��
��1���������1�·ݵ�![]() �����г��ۼ�Ϊ
�����г��ۼ�Ϊ![]() Ԫ/������
Ԫ/������![]() ��ֵ��(���з��̵ķ������)
��ֵ��(���з��̵ķ������)
��2���õ�ƻ�8�·��ٽ�һ��![]() �ͺ�
�ͺ�![]() �����г���50������
�����г���50������![]() �ͳ�����������
�ͳ�����������![]() �ͳ�������2����Ӧ��ν�������ʹ�������г�������ࣿ
�ͳ�������2����Ӧ��ν�������ʹ�������г�������ࣿ
��3���õ�Ϊ������Դ��������һ�ֽ���Ϊ500Ԫ��![]() �ͳ���Ԥ����8��Ԫ���������ֳ�������������
�ͳ���Ԥ����8��Ԫ���������ֳ�������������![]() ����
����![]() �͵�����֮��Ϊ
�͵�����֮��Ϊ![]() ����õ����ٿ��Թ������ֳ�����������
����õ����ٿ��Թ������ֳ�����������
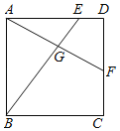
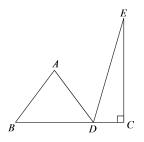
����Ŀ�����κ���![]() ��
��![]() ��
��![]() ��
��![]() �dz�����
�dz�����![]() �����Ա���x�뺯��ֵy�IJ��ֶ�Ӧֵ���±���
�����Ա���x�뺯��ֵy�IJ��ֶ�Ӧֵ���±���
| �� | -1 | 0 | 1 | 3 | �� |
| �� |
| 3 |
| 3 | �� |
�ҵ�![]() ʱ�������Ӧ�ĺ���ֵ
ʱ�������Ӧ�ĺ���ֵ![]() �������н��ۣ���
�������н��ۣ���![]() ����3�ǹ���
����3�ǹ���![]() �ķ���
�ķ���![]() ��һ��������
��һ��������![]() �����У���ȷ���۵ĸ����ǣ� ��
�����У���ȷ���۵ĸ����ǣ� ��
A.0B.1C.2/span>D.3