题目内容
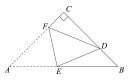
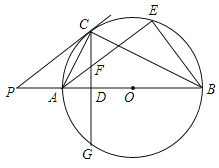
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 平分
平分![]() ,点
,点![]() 是边
是边![]() 上一动点(不与
上一动点(不与![]() 、
、![]() 重合),沿
重合),沿![]() 所在的直线折叠
所在的直线折叠![]() ,点
,点![]() 的对应点为
的对应点为![]() ,当
,当![]() 是直角三角形且
是直角三角形且![]() 为直角边时,则
为直角边时,则![]() 的长为____.
的长为____.
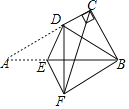
【答案】![]() 或
或![]()
【解析】
分两种情况,当∠BCF=90°时,点F落在AC的延长线上,当∠CBF=90°时,画出图形,由直角三角形的性质可求出答案
∵∠C=90°,∠A=30°,AB=2![]() ,
,
∴BC=![]() AB=
AB=![]() ,
,
∴AC=3,
∵BD平分∠ABC,
∴∠CBD=30°,
∴CD=BCtan30°![]() =1,
=1,
∴BD=AD=2,
如图1,当∠BCF=90°时,点F落在AC的延长线上,
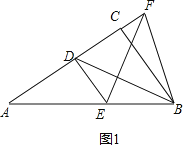
∴∠ADE=90°,
∴AE=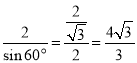 .
.
如图2,当∠CBF=90°,DF=DA=DB,
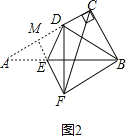
∵∠ACB=∠CBF=90°,
∴BF∥AC,
∴∠DFB=∠DBF=∠ADF=∠BDC=60°,
∵∠ADE=∠EDF,
∴∠ADE=∠A=30°,
∴AE=DE,
过点E作EM⊥AD于点M,
∵AD=2,
∴AM=1,
∴AE=![]() .
.
故答案为:![]() 或
或![]() .
.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某自行车经营店销售![]() 型,
型,![]() 型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
型两种品牌自行车,今年进货和销售价格如下表:(今年1年内自行车的售价与进价保持不变)
|
| |
进货价格(元/辆) | 1000 | 1100 |
销售价格(元/辆) |
| 1500 |
今年经过改造升级后,![]() 型车每辆销售价比去年增加400元.已知
型车每辆销售价比去年增加400元.已知![]() 型车去年1月份销售总额为3.6万元,今年1月份
型车去年1月份销售总额为3.6万元,今年1月份![]() 型车的销售数量与去年1月份相同,而销售总额比去年1月份增加
型车的销售数量与去年1月份相同,而销售总额比去年1月份增加![]() .
.
(1)若设今年1月份的![]() 型自行车售价为
型自行车售价为![]() 元/辆,求
元/辆,求![]() 的值?(用列方程的方法解答)
的值?(用列方程的方法解答)
(2)该店计划8月份再进一批![]() 型和
型和![]() 型自行车共50辆,且
型自行车共50辆,且![]() 型车数量不超过
型车数量不超过![]() 型车数量的2倍,应如何进货才能使这批自行车获利最多?
型车数量的2倍,应如何进货才能使这批自行车获利最多?
(3)该店为吸引客源,准备增购一种进价为500元的![]() 型车,预算用8万元购进这三种车若干辆,其中
型车,预算用8万元购进这三种车若干辆,其中![]() 型与
型与![]() 型的数量之比为
型的数量之比为![]() ,则该店至少可以购进三种车共多少辆?
,则该店至少可以购进三种车共多少辆?