题目内容
已知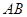 是半径为1的圆
是半径为1的圆 的一条弦,且
的一条弦,且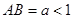 ,以
,以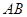 为一边在圆
为一边在圆 内作正三角形
内作正三角形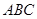 ,点
,点 为圆
为圆 上不同于点
上不同于点 的一点,且
的一点,且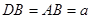 ,
,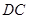 的延长线交圆
的延长线交圆 于点
于点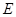 ,求
,求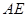 的长。
的长。
 是半径为1的圆
是半径为1的圆 的一条弦,且
的一条弦,且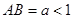 ,以
,以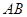 为一边在圆
为一边在圆 内作正三角形
内作正三角形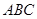 ,点
,点 为圆
为圆 上不同于点
上不同于点 的一点,且
的一点,且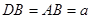 ,
,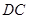 的延长线交圆
的延长线交圆 于点
于点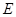 ,求
,求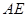 的长。
的长。
1
如图,连接OE,OA,OB。设∠CDB = x°,则∵CD =" AB" = DB, ∴∠BCD = x°。
∵∠ACB = 60°,∴∠ECA =" 120°-" x°。
∵∠ABO =" ∠ABD" / 2 =(∠ABC +∠CBD)/2 = (60°+180°- 2x)/2="120°" - x°,
∴△ACE ≌ △ABO ,AE=" OA" = 1
∵∠ACB = 60°,∴∠ECA =" 120°-" x°。
∵∠ABO =" ∠ABD" / 2 =(∠ABC +∠CBD)/2 = (60°+180°- 2x)/2="120°" - x°,
∴△ACE ≌ △ABO ,AE=" OA" = 1

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
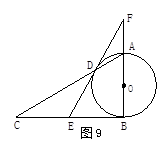
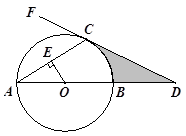

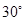 ,则∠A的度数为 ▲ .
,则∠A的度数为 ▲ .

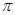 cm,则此扇形的面积为___________.
cm,则此扇形的面积为___________.