题目内容
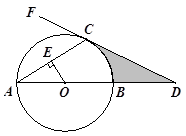
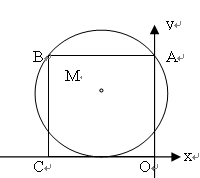
已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
小题1:求证:FD是⊙O的切线;
小题2:设OC与BE相交于点G,若OG=4,求⊙O
半径的长;
小题3:在(2)的条件下,当OE=6时,求图中阴影部分的面积.(结果保留根号)
 |
小题1:求证:FD是⊙O的切线;
小题2:设OC与BE相交于点G,若OG=4,求⊙O
半径的长;
小题3:在(2)的条件下,当OE=6时,求图中阴影部分的面积.(结果保留根号)
小题1:连接OC.∵OA=OC
∴∠A=∠ACO
∵OE⊥AC∠FCA=∠AOE
∴∠A+∠AOE=∠ACO+∠FCA=90°
∴∠FCO=90°
∴FD是⊙O的切线(4分)
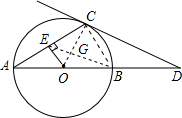
小题2:∵OE⊥AC,AO=CO
∴AE=EC
∵AO=BO
∴OE∥CB且2OE=BC
∴△GEO∽△CGB
∴
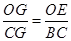
∵OG=4
∴CG=8
OC=CG+OG=12
⊙O半径的长为12. (7分)
小题3:∵OE=6,根据(2)可得BC=12
∵⊙O半径的长为12.
∴△OCB是等边三角形,即∠COB=60°
DC=OCtan∠COB=12
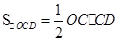 =72
=72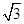 ,
,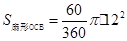 =24
=24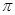
阴影部分的面积.=
 (10分)
(10分)(1)连接OC.欲证明FD是⊙O的切线,只需证明∠FCO=90°;
(2)利用△GEO∽△CGB求出半径;
(3)先求出△OCD面积,再求出扇形OCB面积,这样就能求出阴影面积。
(2)利用△GEO∽△CGB求出半径;
(3)先求出△OCD面积,再求出扇形OCB面积,这样就能求出阴影面积。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目




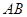 是半径为1的圆
是半径为1的圆 的一条弦,且
的一条弦,且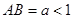 ,以
,以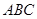 ,点
,点 为圆
为圆 的一点,且
的一点,且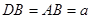 ,
,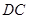 的延长线交圆
的延长线交圆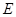 ,求
,求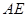 的长。
的长。