题目内容
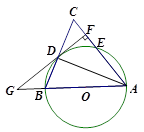
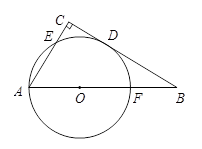
如图9,△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于D点,E为BC的中点,连接ED并延长交BA延长线于F点.
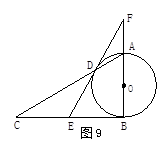
小题1:求证:直线DE是⊙O的切线
小题2:若AB=,AD=1,求线段AF的长
小题3:当D为EF的中点时,试探究线段AB与BC之间的数量关系
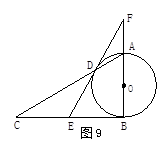
小题1:求证:直线DE是⊙O的切线
小题2:若AB=,AD=1,求线段AF的长
小题3:当D为EF的中点时,试探究线段AB与BC之间的数量关系
小题1:证明:连接OD、BD,则
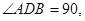
因为
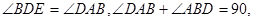
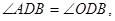 所以
所以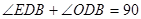 ,则直线DE是⊙O的切线
,则直线DE是⊙O的切线小题2:
小题3:BC=AB
(1)证明:连接OD、BD,则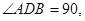
因为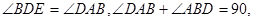
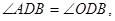 所以
所以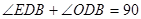 ,则直线DE是⊙O的切线
,则直线DE是⊙O的切线
(2)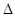 FDA∽
FDA∽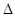 FDB,得
FDB,得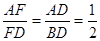 ,设AF=x,则可列方程
,设AF=x,则可列方程
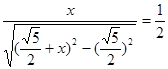 ,解得x=。故AF=。
,解得x=。故AF=。
(3)因为D为EF的中点,∠ABC=90°,所以BD=ED,又点E为BC的中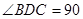 °,所以DE=BE,所以三角形BDE为等边三角形,所以
°,所以DE=BE,所以三角形BDE为等边三角形,所以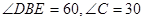 所以tan30=
所以tan30=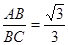
,即BC=AB。
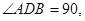
因为
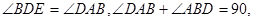
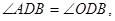 所以
所以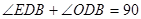 ,则直线DE是⊙O的切线
,则直线DE是⊙O的切线(2)
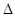 FDA∽
FDA∽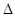 FDB,得
FDB,得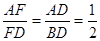 ,设AF=x,则可列方程
,设AF=x,则可列方程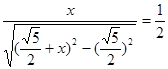 ,解得x=。故AF=。
,解得x=。故AF=。(3)因为D为EF的中点,∠ABC=90°,所以BD=ED,又点E为BC的中
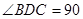 °,所以DE=BE,所以三角形BDE为等边三角形,所以
°,所以DE=BE,所以三角形BDE为等边三角形,所以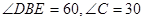 所以tan30=
所以tan30=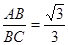
,即BC=AB。

练习册系列答案
相关题目
 的值.
的值.

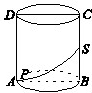
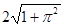 )cm B.(
)cm B.(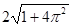 )cm
)cm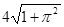 )cm D.(
)cm D.(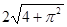 )cm
)cm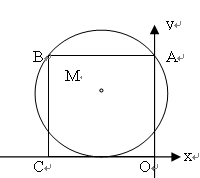
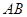 是半径为1的圆
是半径为1的圆 的一条弦,且
的一条弦,且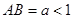 ,以
,以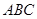 ,点
,点 为圆
为圆 的一点,且
的一点,且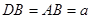 ,
,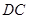 的延长线交圆
的延长线交圆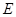 ,求
,求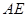 的长。
的长。