Question

【题目】“马踏飞燕”作为商丘的地标性雕塑被拆分为两座雕塑，安放在紧邻高速公路出站口的平原路和华商大道交叉口，不光临近古城景区，也靠近火神台，恰恰实现了商丘市的城市文化宣传的目的．“人们来到商丘，一下高速，就看到商丘的地标，就能够感受到商丘的火文化．”

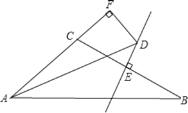
某中学数学兴趣小组准备测量安放后的雕塑相关数据，如图，小明从A点测得“火球”最高点E的仰角为4°30′，此处恰好看不到“马踏飞燕”雕塑的最高点F，小明向雕塑走140m到达点B，此时测得点E的仰角为45°．已知两雕塑的距离为50m，求两座雕塑EC、FD的高度．（A、B、C、D在同一直线上）（精确到1m，参考值：sin4°30′≈0.07，cos4°30′≈0.99，tan4°30′≈0.08．）

Answer 1

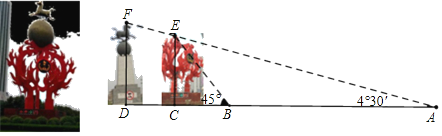
【答案】EC的高度约为12m，FD的高度约为16m．

【解析】

首先证明EC＝CB，设EC＝BC＝x，构建方程求出x，再解直角三角形求出DF即可．

解：在Rt△CEB中，∵∠ECB＝90°，∠EBC＝45°，

∴∠CEB＝∠CBE＝45°，

∴CE＝CB，设EC＝BC＝xm，则AC＝（x+140）m，

∵tanA＝，

∴0.08＝，

解得x≈12，

经检验，x≈12是原方程的解，

∴EC＝12m，

在Rt△ADF中，

∵tanA＝，

∴0.08＝，

∴DF≈16m，

答：两座雕塑EC、FD的高度分别约为12m，16m．