ЬтФПФкШн
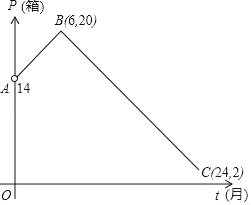
ЁОЬтФПЁПФГжёжЦЦЗМгЙЄГЇИљОнЪаГЁЕїбаНсЙћЃЌЖдИУГЇЩњВњЕФвЛжжаТаЭжёжЦЦЗЭцОпЮДРДСНФъЕФЯњЪлНјаадЄВтЃЌВЂНЈСЂШчЯТФЃаЭЃКЩшЕкtИідТЃЌжёжЦЦЗЯњЪлСПЮЊPЃЈЕЅЮЛЃКЯфЃЉЃЌPгыtжЎМфДцдкШчЭМЫљЪОКЏЪ§ЙиЯЕЃЌЦфЭМЯѓЪЧЯпЖЮABЃЈВЛКЌЕуAЃЉКЭЯпЖЮBCЕФзщКЯЃЎЩшЕкtИідТЯњЪлУПЯфЕФУЋРћШѓЮЊQЃЈАйдЊЃЉЃЌЧвQгыtТњзуШчЯТЙиЯЕQ=2t+8ЃЈ0ЁмtЁм24ЃЉЃЎ
ЃЈ1ЃЉЧѓPгыtЕФКЏЪ§ЙиЯЕЪНЃЈ6ЁмtЁм24ЃЉЃЎ
ЃЈ2ЃЉИУГЇдкЕкМИИідТФмЙЛЛёЕУзюДѓУЋРћШѓЃПзюДѓУЋРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉОЕїВщЗЂЯжЃЌЕБдТУЋРћШѓВЛЕЭгк40000ЧвВЛИпгк43200дЊЪБЃЌИУдТВњЦЗдВФСЯЙЉИјКЭЪаГЁЪлзюКЭаГЃЌДЫЪБГЦетИідТЮЊЁАКЭаГдТЁБЃЌФЧУДЃЌдкЮДРДСНФъжаЕкМИИідТЮЊКЭаГдТЃП
ЁОД№АИЁПЃЈ1ЃЉPЃНЉt+26ЃЈ6ЁмtЁм24ЃЉЃЛЃЈ2ЃЉИУГЇдкЕк11ИідТФмЙЛЛёЕУзюДѓУЋРћШѓЃЌзюДѓУЋРћШѓЪЧ45000дЊЃЛЃЈ3ЃЉЮДРДСНФъжаЕФКЭаГдТгаЃК6ЃЌ7ЃЌ8ЃЌ14ЃЌ15ЃЌ16етСљИідТЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЕБ6ЁмtЁм24ЪБЃЌЩшPгыtЕФКЏЪ§ЙиЯЕЪНЮЊP=kt+bЃЌАбЕуBЃЈ6ЃЌ20ЃЉКЭCЃЈ24ЃЌ2ЃЉДњШыЧѓГіkКЭbЃЌМДПЩЕУНтЃЛ
ЃЈ2ЃЉЩшжБЯпABЕФКЏЪ§НтЮіЪНЮЊP=mt+nЃЌНЋAЃЈ0ЃЌ14ЃЉЃЌB ЃЈ6ЃЌ20ЃЉДњШыЧѓГіmКЭnЃЌЗж0ЃМtЃМ6КЭ6ЁмtЁм24РДЬжТлЧѓНтЃЛ
ЃЈ3ЃЉЗж0ЃМtЃМ6КЭ6ЁмtЁм24ЃЌНсКЯЃЈ2ЃЉжаЧѓЕУЕФУЋРћШѓКЏЪ§ЃЌСаВЛЕШЪНзщПЩНтЃЎ
ЃЈ1ЃЉЕБ6ЁмtЁм24ЪБЃЌЩшPгыtЕФКЏЪ§ЙиЯЕЪНЮЊP=kt+bЃЎ
ЁпИУЭМЯѓЙ§ЕуBЃЈ6ЃЌ20ЃЉКЭCЃЈ24ЃЌ2ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPгыtЕФКЏЪ§ЙиЯЕЪНЮЊP=Љt+26ЃЈ6ЁмtЁм24ЃЉЃЎ
ЃЈ2ЃЉЩшжБЯпABЕФКЏЪ§НтЮіЪНЮЊP=mt+nЃЌНЋAЃЈ0ЃЌ14ЃЉЃЌB ЃЈ6ЃЌ20ЃЉДњШыЕУЃК
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпABЕФКЏЪ§НтЮіЪНЮЊP=t+14ЃЌ
ЁрЕБ0ЃМtЃМ6ЪБЃЌРћШѓL=QP=ЃЈ2t+8ЃЉЃЈt+14ЃЉ=2t2+36t+112=2ЃЈt+9ЃЉ2Љ50ЃЎ
ЕБt=5ЪБЃЌРћШѓLШЁзюДѓжЕЮЊ2ЃЈ5+9ЃЉ2Љ50=342ЃЈАйдЊЃЉ=34200ЃЈдЊЃЉЃЛ
ЕБ6ЁмtЁм24ЪБЃЌРћШѓL=QP=ЃЈ2t+8ЃЉЃЈЉt+26ЃЉ=Љ2t2+44t+208=Љ2ЃЈtЉ11ЃЉ2+450ЃЎ
450АйдЊ=45000дЊЃЌ
ЁрЕБt=11ЪБЃЌРћШѓLгазюДѓжЕЃЌзюДѓжЕЮЊ45000дЊЃЎ
злЩЯЫљЪіЃКИУГЇдкЕк11ИідТФмЙЛЛёЕУзюДѓУЋРћШѓЃЌзюДѓУЋРћШѓЪЧ45000дЊЃЎ
ЃЈ3ЃЉЁп40000дЊ=400АйдЊЃЌ43200дЊ=432АйдЊЃЌ
Ёр![]() Лђ
Лђ![]()
ЕквЛИіВЛЕШЪНЮоНтЃЌЕкЖўИіВЛЕШЪНЕФНтЮЊ6ЁмtЁм8Лђ14ЁмtЁм16ЃЌ
ЁрЮДРДСНФъжаЕФКЭаГдТгаЃК6ЃЌ7ЃЌ8ЃЌ14ЃЌ15ЃЌ16етСљИідТЃЎ

 ЦкФЉБІЕфЕЅдЊМьВтЗжРрИДЯАОэЯЕСаД№АИ
ЦкФЉБІЕфЕЅдЊМьВтЗжРрИДЯАОэЯЕСаД№АИЁОЬтФПЁПгавЛИідВаЮзЊХЬЃЌЗжКкЩЋЁЂАзЩЋСНИіЧјгђЃЎ
ЃЈ1ЃЉФГШЫзЊЖЏзЊХЬЃЌЖджИеыТфдкКкЩЋЧјгђЛђАзЩЋЧјгђНјааСЫДѓСПЪдбщЃЌЕУЕНЪ§ОнШчЯТБэЃК
ЪЕбщДЮЪ§ | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
АзЩЋЧјгђДЮЪ§ | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
ТфдкАзЩЋЧјгђЦЕТЪ | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
ЧыФуРћгУЩЯЪіЪЕбщЃЌЙРМЦзЊЖЏИУзЊХЬжИеыТфдкАзЩЋЧјгђЕФИХТЪЮЊ___________ЃЎ(ОЋШЗЕН0.01)ЃЛ
ЃЈ2ЃЉШєИУдВаЮзЊХЬАзЩЋЩШаЮЕФдВаФНЧЮЊ120ЖШЃЌКкЩЋЩШаЮЕФдВаФНЧЮЊ![]() ЃЌзЊЖЏзЊХЬСНДЮЃЌЧѓжИеывЛДЮТфдкАзЩЋЧјгђЃЌСэвЛДЮТфдкКкЩЋЧјгђЕФИХТЪЃЎ
ЃЌзЊЖЏзЊХЬСНДЮЃЌЧѓжИеывЛДЮТфдкАзЩЋЧјгђЃЌСэвЛДЮТфдкКкЩЋЧјгђЕФИХТЪЃЎ