题目内容
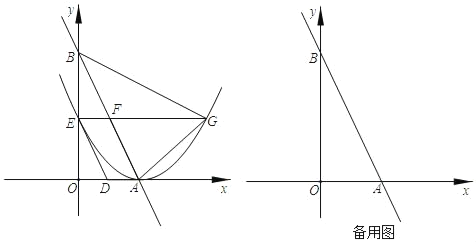
【题目】已知:如图,在△ABC中,点D、E分别在边BC和AB上,且AD=AC,EB=ED,分别延长ED、AC交于点F.

(1)求证:△ABD∽△FDC;
(2)求证:AE2=BEEF.
【答案】(1)见详解;(2)见详解;
【解析】
(1)根据等腰三角形的性质得到∠ADC=∠ACD,∠B=∠BDE,根据三角形的外角的性质得到∠BAD=∠F,于是得到结论;
(2)根据相似三角形的性质得到![]() ,等量代换即可得到结论.
,等量代换即可得到结论.
证明:(1)∵AD=AC,
∴∠ADC=∠ACD,
∵BE=DE,
∴∠B=∠BDE,
∵∠BDE=∠CDF,
∴∠CDF=∠B,
∵∠BAD=∠ADC﹣∠B,∠F=∠ACD﹣∠CDF,
∴∠BAD=∠F,
∴△ABD∽△FDC;
(2)∵∠EAD=∠F,∠AED=∠FEA,
∴△AED∽△FEA,
∴![]() ,
,
∴AE2=DEEF,
∵BE=DE,
∴AE2=BEEF.

练习册系列答案
相关题目