题目内容
【题目】将一个正方形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() ,点
,点![]() ,
,![]() ,
,![]() 点.动点
点.动点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上,沿
上,沿![]() 折叠该纸片,使点
折叠该纸片,使点![]() 的对应点
的对应点![]() 始终落在边
始终落在边![]() 上(点
上(点![]() 不与
不与![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,
处,![]() 与
与![]() 交于点
交于点![]() .
.
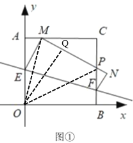
(Ⅰ)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
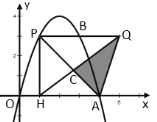
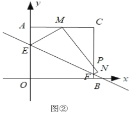
(Ⅱ)如图②,当点![]() 落在
落在![]() 的中点时,求点
的中点时,求点![]() 的坐标;
的坐标;
(Ⅲ)随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
的周长是否发生变化?如变化,简述理由;如不变,直接写出其值.
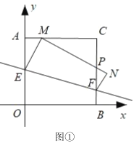
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)不变,
;(Ⅲ)不变,![]() 的周长为8.
的周长为8.
【解析】
(Ⅰ)根据含30°直角三角形的性质以及勾股定理,在Rt△AEM中运用勾股定理列出方程即可解答;
(Ⅱ)由题意可得AM=MC=2,设AE=a,则OE=EM=4-a,在Rt△AEM中,利用勾股定理列出方程即可解答;
(Ⅲ)如图,连接OM,OP,过点O作OQ⊥MP于点Q,由折叠的性质及平行线的性质得到∠MOB=∠OMP,进而证明△AMO≌△QMO(AAS),得到AM=QM,AO=QO,再证明Rt△QOP≌Rt△BOP(HL),得到QP=BP,将△MPC的周长进行转化即可得到AC+BC=8即可.
解:(Ⅰ)当![]() 时,
时,
∵四边形AOBC是正方形,
∴∠OAC=90°,
∴AM=![]() ,
,
由折叠可知,OE=EM,
设AM=x,则EM=OE=2x,
∵![]() ,
,
∴OA=4,
∴AE=4-2x,
在Rt△AEM中,AM2+AE2=EM2,
即![]() ,解得:
,解得:![]() ,
,![]() (舍去)
(舍去)
∴OE=2x=![]() ,
,
∴![]() ;
;
(Ⅱ)∵AC=4,
∴当点![]() 落在
落在![]() 的中点时,AM=MC=2,
的中点时,AM=MC=2,
设AE=a,则OE=EM=4-a,
则在Rt△AEM中,AM2+AE2=EM2,
即![]() ,解得:
,解得:![]() ,
,
∴OE=![]() ,
,
∴![]() ;
;
(Ⅲ)不变,![]() 的周长为8,
的周长为8,
如图,连接OM,OP,过点O作OQ⊥MP于点Q,
由折叠可知,∠EMP=∠AOB=90°,OE=EM,
∴∠EOM=∠EMO,
∴90°-∠EOM=90°-∠EMO,即∠MOB=∠OMP,
又∵正方形AOBC中,AC∥OB,
∴∠AMO=∠MOB,
∴∠AMO=∠OMP,
在△AMO与△QMO中,
∠OAM=∠OQM=90°,∠AMO=∠OMQ,OM=OM,
∴△AMO≌△QMO(AAS),
∴AM=QM,AO=QO,
又∵AO=BO,
∴QO=BO,
∴在Rt△QOP与Rt△BOP中,
OP=OP,QO=BO,
∴Rt△QOP≌Rt△BOP(HL),
∴QP=BP,
∴![]() 的周长=MC+PC+MP
的周长=MC+PC+MP
=MC+PC+MQ+QP
=MC+AM+PC+BP
=AC+BC
=8
∴随着点![]() 在
在![]() 边上位置的变化,
边上位置的变化,![]() 的周长不变,周长为8.
的周长不变,周长为8.