题目内容
【题目】二次函数y＝ax2＋bx＋c（a，b，c 为常数，且a≠0）的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | －1 | 0 | 1 | 2 | 3 | … |
y | … | －3 | －3 | －1 | 3 | 9 | … |
关于x的方程ax2＋bx＋c＝0一个负数解x1满足k＜x1＜k+1（k为整数），则k＝________．
【答案】－3
【解析】
首先利用表中的数据求出二次函数，再利用求根公式解得x1，再利用夹逼法可确定x1的取值范围，可得k．
解:把x=0,y=-3,x=1,y=-1,x=-1,y=-3代入y＝ax2＋bx＋c得
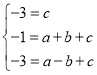，解得
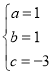，∴y=x+x-3,
∵△=b2-4ac=12-4×1×（-3）=13，
∴x=
=1±
，
∵
<0,
∴=1-＜0，
∵-4≤-
≤-3，
∴
，
∴-3≤1≤
，
∵整数k满足k＜x1＜k+1，
∴k=-3，
故答案为:-3．
练习册系列答案
相关题目
