题目内容
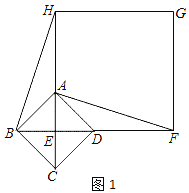
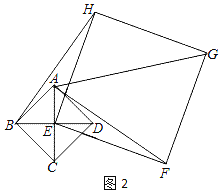
【题目】如图,四边形ABCD中,AD=BC,AB=CD,E,F分别是AB,CD上的点,且∠DAF=∠BCE,
(1)求证:AE=CF;
(2)若将此题中的条件改为:“E,F分别是AB,CD延长线上的点”,其余条件不变,此时,∠ABC=60°,∠BEC=40°,作∠ABC的平分线BN交AF于M,交AD于N,求∠AMN的度数(要求:画示意图,不写画法,写推理过程)
【答案】(1)见解析;(2)10°
【解析】分析:(1)易得四边形ABCD是平行四边形,那么∠D=∠B,易得△ADF≌△CBE,那么BE=DF,∴AE=CF;
(2)利用外角等于和它不相邻的2个内角的和可得∠BCE的度数,也就求得了∠DAF的度数,利用角平分线定义易得∠NBC的度数,也就求得了∠MND的度数,利用三角形的外角的性质即可求得∠AMN的度数.
详解:(1)∵AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴∠D=∠B,
∵∠DAF=∠BCE,
∴△ADF≌△CBE,
∴BE=DF,
∴AE=CF;
(2)∵∠ABM=∠CBM=![]() ∠ABC=30°,
∠ABC=30°,
又∵AD∥BC
∴∠MND=∠CBM=30°
∵∠ABC=∠E+∠BCE,
∴∠BCE=∠ABC﹣∠E=60°﹣40°=20°
∴∠FAD=∠BCE=20°
又∵∠MND=∠FAD+∠AMN
∴∠AMN=∠MND﹣∠FAD=30°﹣20°=10°.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目