题目内容
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

【答案】(1)y=-2x+8 ;(2)P(0,5) 3
【解析】试题分析:(1)将A点坐标代入反比例函数解析式即可求出m的值,再将x=3代入反比例函数解析式解得n的值,由此得出B点的坐标,结合A、B两点的坐标,利用待定系数法即可求出一次函数的表达式;
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,在y轴上任选一点不同于P点的P′点,由三角形内两边之和大于第三边来验证点P就是我们找到的使得PA+PB的值最小的点,由A点的坐标找出点A′的坐标,由待定系数法可求出直线A′B的函数表达式,令x=0即可得出P点的坐标;再结合三角形的面积公式与点到直线的距离即可求出△PAB的面积.
试题解析:解:(1)将点A(1,6)代入反比例函数![]() 中,得6=
中,得6=![]() ,即m=6.
,即m=6.
故反比例函数的解析式为![]() .
.
∵点B(3,n)在反比例函数![]() 上,∴n=
上,∴n=![]() =2.即点B的坐标为(3,2).
=2.即点B的坐标为(3,2).
将点A(1,6)、点B(3,2)代入y=kx+b中,得: ![]() ,解得:
,解得: ![]() .
.
故一次函数的解析式为y=﹣2x+8.
(2)作点A关于y轴的对称点A′,连接A′B交y轴于点P,如图1所示.
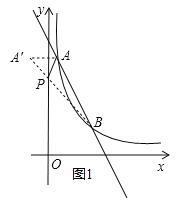
在y轴上任取一点P′(不同于点P).∵A、A′关于y轴对称,∴AP=A′P,AP′=A′P′.在△P′A′B中,有A′P′+BP′=AP′+BP′>A′B=A′P+BP=AP+BP,∴当A′、P、B三点共线时,PA+PB最小.
∵点A的坐标为(1,6),∴点A′的坐标为(﹣1,6).
设直线A′B的解析式为y=ax+b,将点A′(﹣1,6)、点B(3,2)代入到y=ax+b中,得: ![]() ,解得:
,解得: ![]() ,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
,∴直线A′B的解析式为y=﹣x+5,令x=0,则有y=5.
即点P的坐标为(0,5).
直线AB解析式为y=﹣2x+8,即2x+y﹣8=0.
AB=![]() =
=![]() ,点P到直线AB的距离d=
,点P到直线AB的距离d=![]() =
=![]() .
.
△PAB的面积S=![]() ABD=
ABD=![]() ×
×![]() ×
×![]() =3.
=3.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案