题目内容
【题目】如图,点B(3,3)在双曲线y=![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,DM⊥x轴于M,BN⊥x轴于N,且点A、 B、 C、D构成的四边形为正方形.
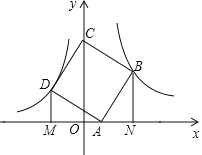
(1)k的值为___;
(2)求证:△ADM≌△BAN;
(3)求点A的坐标.
【答案】(1)9;(2)证明见解析;(3)A(1,0);
【解析】
(1)把点B(3,3)代入双曲线y=![]() (x>0),求出k的值即可;
(x>0),求出k的值即可;
(2)由四边形ABCD为正方形,利用正方形的性质得到AD=AB,且∠DAB为直角,利用同角的余角相等得到一对角相等,再由一对直角相等,利用AAS即可得证;
(3)由△ADM≌△BAN得到DM=AN,AM=BN,根据B的坐标得到ON=BN=3,设A(a,0),即OA=a,由ON﹣OA表示出AN,即为DM,为D的纵坐标,代入反比例解析式表示出横坐标,确定出OM,由OM+OA表示出AM,根据AM=BN=3求出a的值,即可确定出A坐标.
(1)∵点B(3,3)在双曲线y=![]() (x>0)上,∴k=3×3=9.
(x>0)上,∴k=3×3=9.
故答案为:9;
(2)∵四边形ABCD为正方形,∴∠DAB=90°,AD=AB,∴∠DAM+∠BAN=90°.
∵∠MDA+∠DAM=90°,∴∠MDA=∠BAN.
在△ADM和△BAN中,∵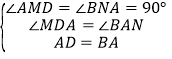 ,∴△ADM≌△BAN(AAS);
,∴△ADM≌△BAN(AAS);
(3)∵△ADM≌△BAN,∴AN=DM,BN=AM,设A(a,0),即OA=a.
∵B(3,3),∴BN=ON=3,∴DM=AN=ON﹣OA=3﹣a,把y=3﹣a代入y=﹣![]() ,得:x=﹣
,得:x=﹣![]() ,即OM=
,即OM=![]() ,∴BN=AM=OM+OA=
,∴BN=AM=OM+OA=![]() +a=3,解得:a=1或a=5(不合题意,舍去),∴A(1,0).
+a=3,解得:a=1或a=5(不合题意,舍去),∴A(1,0).

【题目】为了落实党的“精准扶贫”政策,A,B两城决定向C,D两乡运送肥料以支持农村生产.已知A,B两城分别有肥料210吨和290吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C,D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)设从A城运往C乡肥料x吨.
①用含x的代数式完成下表:
C乡(吨) | D乡(吨) | |
A城 | x | |
B城 | ||
总计 | 240 | 260 |
②设总运费为y元,写出y与x的函数关系式,并求出最少总运费;
(2)由于更换车型,使从A城往C乡运肥料的费用每吨减少a(![]() )元,这时从A城往C乡运肥料多少吨时总运费最少?
)元,这时从A城往C乡运肥料多少吨时总运费最少?